参考和摘录以下博客,对作者的贡献表示感谢,欢迎参考以下文章!
https://blog.csdn.net/qq_39422642/article/details/78676567
https://zhuanlan.zhihu.com/p/28054589
https://blog.csdn.net/qq_16234613/article/details/79476763
http://www.cnblogs.com/pinard/p/6509630.html
https://zhuanlan.zhihu.com/p/28687529
http://www.cnblogs.com/pinard/p/6509630.html
https://zhuanlan.zhihu.com/p/26892413
https://zhuanlan.zhihu.com/p/21462488?refer=intelligentunit
目录
循环神经网络的应用比较多,比如能写文章,写程序,写诗歌,但是很多训练出来的结果还不能令人满意,要想真正让它更有用,路还很远。
我们一般的见过的神经网络的结构:
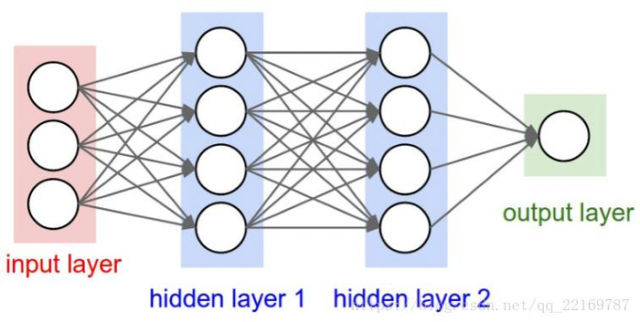
既然我们已经有了人工神经网络和卷积神经网络,为什么还要循环神经网络?
原因很简单,无论是卷积神经网络,还是人工神经网络,他们的前提假设都是:元素之间是相互独立的,输入与输出也是独立的,比如猫和狗。
但现实世界中,很多元素都是相互连接的,比如,一个人说了:我是中国人,我的母语是_____.这里填空,人应该都知道是填“汉语“。因为我们是根据上下文的内容推断出来的,但机会要做到这一步就相当得难了。因此,就有了现在的循环神经网络,他的本质是:像人一样拥有记忆的能力。因此,他的输出就依赖于当前的输入和记忆。
它的网络结构如下:
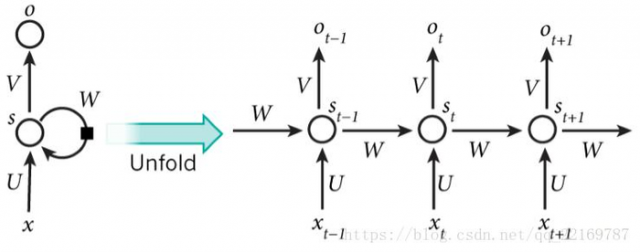
其中每个圆圈可以看作是一个单元,而且每个单元做的事情也是一样的,因此可以折叠呈左半图的样子。用一句话解释RNN,就是一个单元结构重复使用。
RNN是一个序列到序列的模型,假设xt−1,xt,xt+1xt−1,xt,xt+1是一个输入:“我是中国“,那么ot−1,otot−1,ot就应该对应”是”,”中国”这两个,预测下一个词最有可能是什么?就是ot+1ot+1应该是”人”的概率比较大。
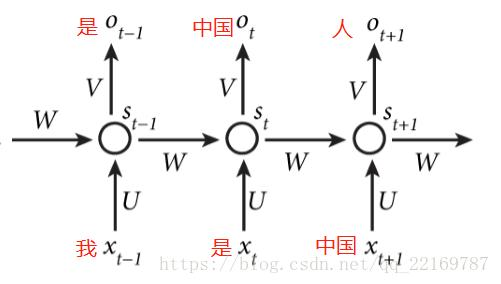
因此,我们可以做这样的定义:
Xt:表示t时刻的输入,ot:表示t时刻的输出,St:表示t时刻的记忆,St是时间t处的“记忆”,St=f(U*Xt+W*St−1),f可以是tanh等
因为我们当前时刻的输出是由记忆和当前时刻的输入决定的,就像你现在大四,你的知识是由大四学到的知识(当前输入)和大三以及大三以前学到的东西的(记忆)的结合,RNN在这点上也类似,神经网络最擅长做的就是通过一系列参数把很多内容整合到一起,然后学习这个参数,因此就定义了RNN的基础。
大家可能会很好奇,为什么还要加一个f()函数,其实这个函数是神经网络中的**函数,但为什么要加上它呢?
举个例子,假如你在大学学了非常好的解题方法,那你初中那时候的解题方法还要用吗?显然是不用了的。RNN的想法也一样,既然我能记忆了,那我当然是只记重要的信息啦,其他不重要的,就肯定会忘记,是吧。但是在神经网络中什么最适合过滤信息呀?肯定是**函数嘛,因此在这里就套用一个**函数,来做一个非线性映射,来过滤信息,这个**函数可能为tanh,也可为其他。
假设你大四快毕业了,要参加考研,请问你参加考研是不是先记住你学过的内容然后去考研,还是直接带几本书去参加考研呢?很显然嘛,那RNN的想法就是预测的时候带着当前时刻的记忆St去预测。假如你要预测“我是中国“的下一个词出现的概率,这里已经很显然了,运用softmax来预测每个词出现的概率再合适不过了,但预测不能直接带用一个矩阵来预测呀,所有预测的时候还要带一个权重矩阵V,用公式表示为:
ot=softmax(V*St)
其中ot就表示时刻t的输出。
RNN中的结构细节:
1.可以把St当作隐状态,捕捉了之前时间点上的信息。就像你去考研一样,考的时候记住了你能记住的所有信息。
2.otot是由当前时间以及之前所有的记忆得到的。就是你考研之后做的考试卷子,是用你的记忆得到的。
3.很可惜的是,StSt并不能捕捉之前所有时间点的信息。就像你考研不能记住所有的英语单词一样。
4.和卷积神经网络一样,这里的网络中每个cell都共享了一组参数(U,V,W),这样就能极大的降低计算量了。
5.otot在很多情况下都是不存在的,因为很多任务,比如文本情感分析,都是只关注最后的结果的。就像考研之后选择学校,学校不会管你到底怎么努力,怎么心酸的准备考研,而只关注你最后考了多少分。
在有些情况,比如有一部电视剧,在第三集的时候才出现的人物,现在让预测一下在第三集中出现的人物名字,你用前面两集的内容是预测不出来的,所以你需要用到第四,第五集的内容来预测第三集的内容,这就是双向RNN的想法。如图是双向RNN的图解:
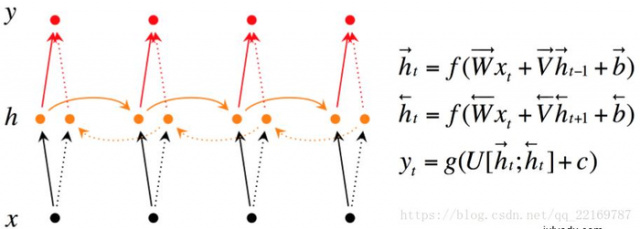
双向RNN需要的内存是单向RNN的两倍,因为在同一时间点,双向RNN需要保存两个方向上的权重参数,在分类的时候,需要同时输入两个隐藏层输出的信息。
深层双向RNN 与双向RNN相比,多了几个隐藏层,因为他的想法是很多信息记一次记不下来,比如你去考研,复习考研英语的时候,背英语单词一定不会就看一次就记住了所有要考的考研单词吧,你应该也是带着先前几次背过的单词,然后选择那些背过,但不熟的内容,或者没背过的单词来背吧。
深层双向RNN就是基于这么一个想法,他的输入有两方面,第一就是前一时刻的隐藏层传过来的信息h→(i)t−1h→t−1(i),和当前时刻上一隐藏层传过来的信息h(i−1)t=[h→(i−1)t;h←(i−1)t]ht(i−1)=[h→t(i−1);h←t(i−1)],包括前向和后向的。
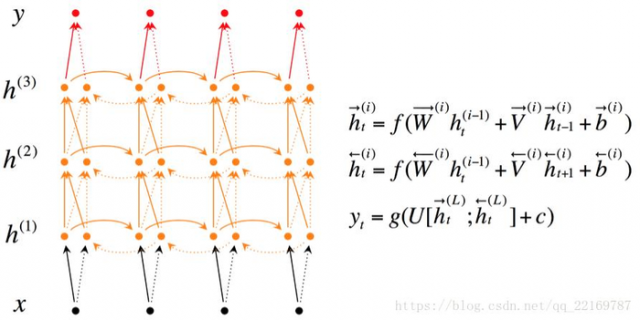
如前面我们讲的,如果要预测t时刻的输出,我们必须先利用上一时刻(t-1)的记忆和当前时刻的输入,得到t时刻的记忆:
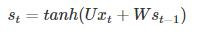
然后利用当前时刻的记忆,通过softmax分类器输出每个词出现的概率:
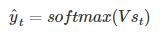
为了找出模型最好的参数,U,W,V,我们就要知道当前参数得到的结果怎么样,因此就要定义我们的损失函数,用交叉熵损失函数:
t时刻的损失: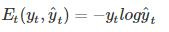
其中yt t时刻的标准答案,是一个只有一个是1,其他都是0的向量;y^t是我们预测出来的结果,与yt的维度一样,但它是一个概率向量,里面是每个词出现的概率。因为对结果的影响,肯定不止一个时刻,因此需要把所有时刻的造成的损失都加起来:
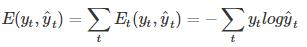
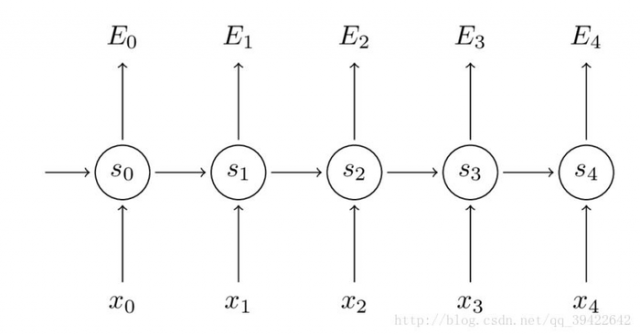
如图所示,你会发现每个cell都会有一个损失,我们已经定义好了损失函数,接下来就是熟悉的一步了,那就是根据损失函数利用SGD来求解最优参数,在CNN中使用反向传播BP算法来求解最优参数,但在RNN就要用到BPTT,它和BP算法的本质区别,也是CNN和RNN的本质区别:CNN没有记忆功能,它的输出仅依赖与输入,但RNN有记忆功能,它的输出不仅依赖与当前输入,还依赖与当前的记忆。这个记忆是序列到序列的,也就是当前时刻收到上一时刻的影响,比如股市的变化。
因此,在对参数求偏导的时候,对当前时刻求偏导,一定会涉及前一时刻,我们用例子看一下:
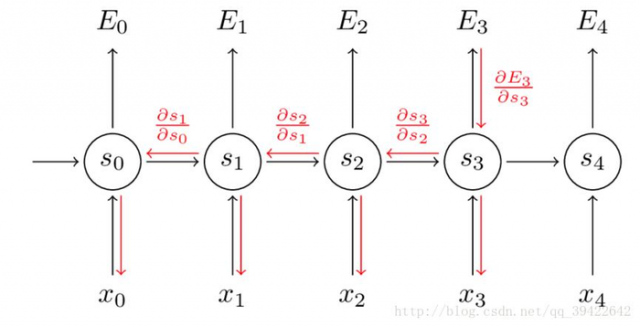
假设我们对E3E3的W求偏导:它的损失首先来源于预测的输出y^3y^3,预测的输出又是来源于当前时刻的记忆s3s3,当前的记忆又是来源于当前的输出和截止到上一时刻的记忆:s3=tanh(Ux3+Ws2)
因此,根据链式法则可以有:
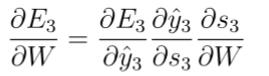
但是,你会发现,s2=tanh(Ux2+Ws1),也就是s2里面的函数还包含了W,因此,这个链式法则还没到底,就像图上画的那样,所以真正的链式法则是这样的:
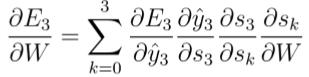
我们要把当前时刻造成的损失,和以往每个时刻造成的损失加起来,因为我们每一个时刻都用到了权重参数W。和以往的网络不同,一般的网络,比如人工神经网络,参数是不同享的,但在循环神经网络,和CNN一样,设立了参数共享机制,来降低模型的计算量。
以下为转载另一篇文章的RNN的训练方法——BPTT:https://blog.csdn.net/zhaojc1995/article/details/80572098
BPTT(back-propagation through time)算法是常用的训练RNN的方法,其实本质还是BP算法,只不过RNN处理时间序列数据,所以要基于时间反向传播,故叫随时间反向传播。BPTT的中心思想和BP算法相同,沿着需要优化的参数的负梯度方向不断寻找更优的点直至收敛。综上所述,BPTT算法本质还是BP算法,BP算法本质还是梯度下降法,那么求各个参数的梯度便成了此算法的核心。 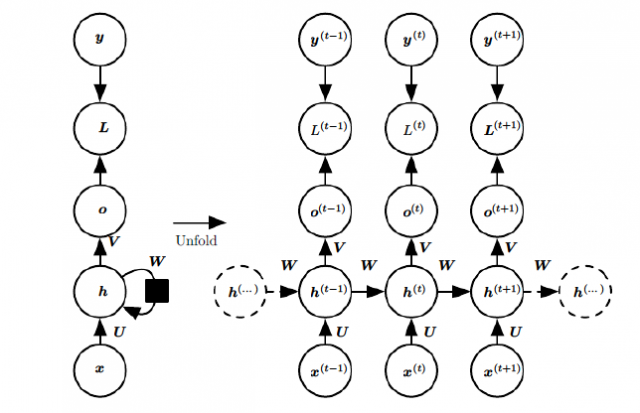
再次拿出这个结构图观察,需要寻优的参数有三个,分别是U、V、W。与BP算法不同的是,其中W和U两个参数的寻优过程需要追溯之前的历史数据,参数V相对简单只需关注目前,那么我们就来先求解参数V的偏导数。
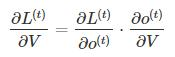
这个式子看起来简单但是求解起来很容易出错,因为其中嵌套着**函数函数,是复合函数的求道过程。
RNN的损失也是会随着时间累加的,所以不能只求t时刻的偏导。
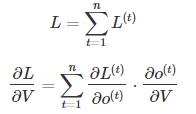
W和U的偏导的求解由于需要涉及到历史数据,其偏导求起来相对复杂,我们先假设只有三个时刻,那么在第三个时刻 L对W的偏导数为:
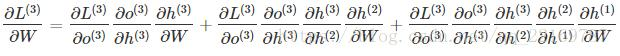
相应的,L在第三个时刻对U的偏导数为:
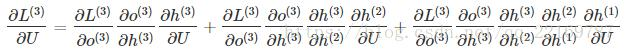
可以观察到,在某个时刻的对W或是U的偏导数,需要追溯这个时刻之前所有时刻的信息,这还仅仅是一个时刻的偏导数,上面说过损失也是会累加的,那么整个损失函数对W和U的偏导数将会非常繁琐。虽然如此但好在规律还是有迹可循,我们根据上面两个式子可以写出L在t时刻对W和U偏导数的通式:
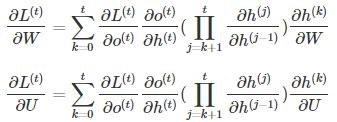
整体的偏导公式就是将其按时刻再一一加起来。
前面说过**函数是嵌套在里面的,如果我们把**函数放进去,拿出中间累乘的那部分:
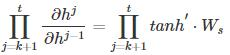
或是
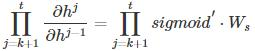
我们会发现累乘会导致**函数导数的累乘,进而会导致“梯度消失“和“梯度爆炸“现象的发生。
至于为什么,我们先来看看这两个**函数的图像。
这是sigmoid函数的函数图和导数图。 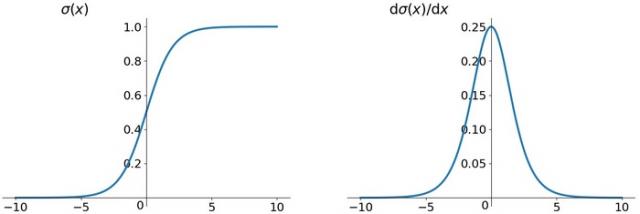
这是tanh函数的函数图和导数图。 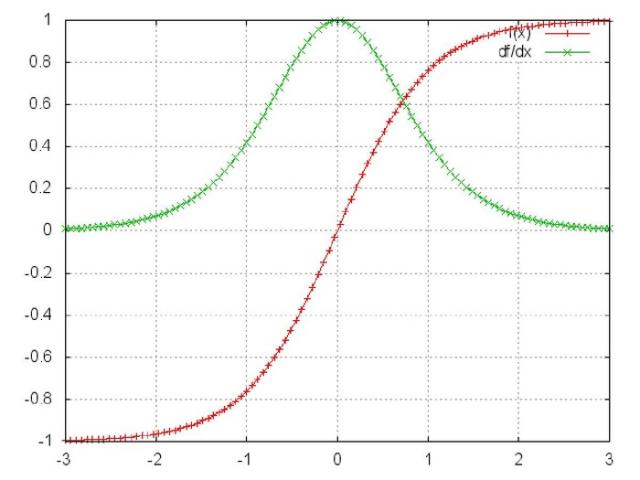
它们二者是何其的相似,都把输出压缩在了一个范围之内。他们的导数图像也非常相近,我们可以从中观察到,sigmoid函数的导数范围是(0,0.25],tach函数的导数范围是(0,1],他们的导数最大都不大于1。
这就会导致一个问题,在上面式子累乘的过程中,如果取sigmoid函数作为**函数的话,那么必然是一堆小数在做乘法,结果就是越乘越小。随着时间序列的不断深入,小数的累乘就会导致梯度越来越小直到接近于0,这就是“梯度消失“现象。其实RNN的时间序列与深层神经网络很像,在较为深层的神经网络中使用sigmoid函数做**函数也会导致反向传播时梯度消失,梯度消失就意味消失那一层的参数再也不更新,那么那一层隐层就变成了单纯的映射层,毫无意义了,所以在深层神经网络中,有时候多加神经元数量可能会比多家深度好。
你可能会提出异议,RNN明明与深层神经网络不同,RNN的参数都是共享的,而且某时刻的梯度是此时刻和之前时刻的累加,即使传不到最深处那浅层也是有梯度的。这当然是对的,但如果我们根据有限层的梯度来更新更多层的共享的参数一定会出现问题的,因为将有限的信息来作为寻优根据必定不会找到所有信息的最优解。
之前说过我们多用tanh函数作为**函数,那tanh函数的导数最大也才1啊,而且又不可能所有值都取到1,那相当于还是一堆小数在累乘,还是会出现“梯度消失“,那为什么还要用它做**函数呢?原因是tanh函数相对于sigmoid函数来说梯度较大,收敛速度更快且引起梯度消失更慢。
还有一个原因是sigmoid函数还有一个缺点,Sigmoid函数输出不是零中心对称。sigmoid的输出均大于0,这就使得输出不是0均值,称为偏移现象,这将导致后一层的神经元将上一层输出的非0均值的信号作为输入。关于原点对称的输入和中心对称的输出,网络会收敛地更好。
RNN的特点本来就是能“追根溯源“利用历史数据,现在告诉我可利用的历史数据竟然是有限的,这就令人非常难受,解决“梯度消失“是非常必要的。解决“梯度消失“的方法主要有:
1、选取更好的**函数
2、改变传播结构
关于第一点,一般选用ReLU函数作为**函数,ReLU函数的图像为: 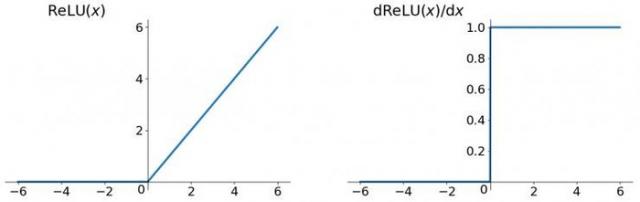
ReLU函数的左侧导数为0,右侧导数恒为1,这就避免了“梯度消失“的发生。但恒为1的导数容易导致“梯度爆炸“,但设定合适的阈值可以解决这个问题。还有一点就是如果左侧横为0的导数有可能导致把神经元学死,不过设置合适的步长(学习旅)也可以有效避免这个问题的发生。
关于第二点,LSTM结构可以解决这个问题。
总结一下,sigmoid函数的缺点:
1、导数值范围为(0,0.25],反向传播时会导致“梯度消失“。tanh函数导数值范围更大,相对好一点。
2、sigmoid函数不是0中心对称,tanh函数是,可以使网络收敛的更好。
本文链接:http://task.lmcjl.com/news/12080.html