提到排序算法，多数人最先想到的就是快速排序算法。快速排序算法是在分治算法基础上设计出来的一种排序算法，和其它排序算法相比，快速排序算法具有效率高、耗费资源少、容易实现等优点。

快速排序算法的实现思路是：

• 从待排序序列中任选一个元素（假设为 pivot）作为中间元素，将所有比 pivot 小的元素移动到它的左边，所有比 pivot 大的元素移动到它的右边；
• pivot 左右两边的子序列看作是两个待排序序列，各自重复执行第一步。直至所有的子序列都不可再分（仅包含 1 个元素或者不包含任何元素），整个序列就变成了一个有序序列。

举个例子，使用快速排序算法对 {35, 33, 42, 10, 14, 19, 27, 44, 26, 31} 进行升序排序的过程为：
1) 选择序列中最后一个元素 31 作为中间元素，将剩余元素分为两个子序列，如下图所示：

分得的两个子序列是 {26, 27, 19, 10, 14} 和 {33, 44, 35, 42}，前者包含的所有元素都比 31 小，后者包含的所有元素都比 31 大，两个子序列还可以再分。

2) 重复第一步，将 {26, 27, 19, 10, 14} 看作新的待排序序列：

1. 选择最后一个元素 14 作为中间元素，将剩余元素分为 {10} 和 {19, 26, 27} 两个子序列。其中 {10} 仅有一个元素，无法再分；{19, 26, 27} 可以再分。
2. 将 {19, 26, 27} 看作新的待排序序列，选择最后一个元素 27 作为中间元素，分得的两个子序列为 {19, 26} 和 {}。其中 {} 是空序列，无法再分；{19, 26} 可以再分。
3. 将 {19, 26} 看作新的待排序序列，选择最后一个元素 26 作为中间元素，分得的两个子序列为 {19} 和 {}，两个子序列都无法再分。

经过以上 3 步， {26, 27, 19, 10, 14} 子序列变成了 {10, 14, 19, 26, 27}，这是一个有序的子序列。

3、重复第一步，将 {33, 44, 35, 42} 看作新的待排序序列：

1. 选择最后一个元素 42 作为中间元素，将剩余元素分为 {33, 35} 和 {44} 两个子序列。其中 {33, 35} 可以再分；{44} 仅有一个元素，无法再分。
2. 将 {33, 35} 看作新的待排序序列，选择最后一个元素 35 作为中间元素，分得的两个子序列为 {33} 和 {}，两个子序列都无法再分。

经过以上 2 步， {33, 44, 35, 42} 子序列变成了 {33, 35, 42, 44}，这是一个有序的子序列。

最终，原序列变成了 {10, 14, 19, 26, 27, 31, 33, 35, 42, 44}，这是一个升序序列。如下是整个过程对应的伪代码：

输入 arr[]                              // 输入待排序序列
quick_sort(arr[] , p , q):              // [p , q] 用于指定当前要处理的子序列
    if q-p <= 0:                        // 如果序列中没有元素或者仅包含 1 个元素，则直接返回
        return
    else:
        par <- partition(arr , p , q)   // partition()函数用于将 [p,q] 区域分割成 [p, par-1] 和 [par+1, q] 区域，[p, par-1] 区域的元素都比 pivot 小，[par+1 , q] 区域的元素都比 pivot 大，函数会返回中间元素 pivot 所在的位置。
        quick_sort(arr , p , par-1)     // 将 [p , par-1] 作为待排序序列，重复进行分割
        quick_sort(arr , par+1 , q)     // 将 [par+1 , q] 作为待排序序列，重复进行分割

借助伪代码，我们了解了快速排序的实现过程，接下来要解决的问题是如何设计 partition() 函数，即如何将 [p, q] 区域的待排序序列分成 [p, par-1] 和 [par+1, q] 两个子序列，同时保证 [p, par-1] 区域内的所有元素比 par 位置上的元素小，[par+1, q] 区域内的所有元素比 par 位置上的元素大？

这里给大家讲解一种方法，以 {35, 33, 42, 10, 14, 19, 27, 44, 26, 31} 为例，选择 31 作为中间元素，具体的实现过程为：
1) 建立 2 个指针（命名为 lo 和 hi），分别指向序列中第一个元素和倒数第 2 个元素，如下图所示：

2) lo 指针向右移动，当指向的元素不小于 31 时暂停。显然，当前指向的 35 > 31，所以 lo 暂时不移动；

3) hi 指针向左移动，当指向的元素不大于 31 时暂停。显然，当前指向的 26< 31，所以 hi 暂时不移动；

4) 交换 lo 和 hi 所指元素的位置，如下图所示：

5) 重复执行 2~4 步，直至 lo ≥ hi。此时，将 pivot 元素与 lo 所指元素交换位置。下面的动画演示了整个分割的过程：

可以看到，最终元素 31 左侧的元素都比它小，右侧的元素都比它大。如下是实现 partition() 函数的伪代码：

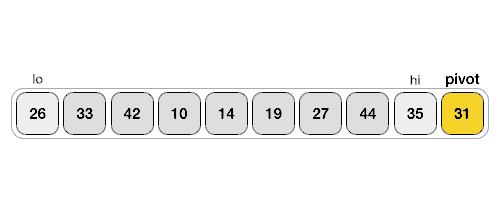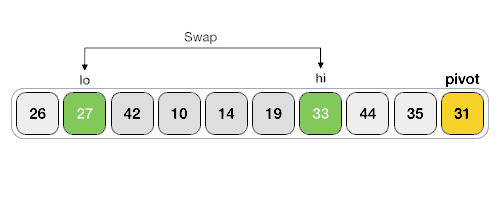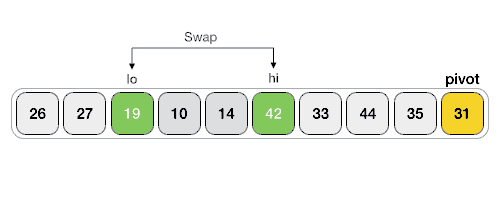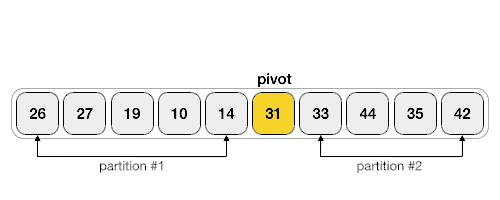
partition(arr[] , p , q):              // [p , q] 为要分割的区域
    lo <- p                            // lo、hi 准备遍历 [p , q-1] 区域
    hi <- q-1
    pivot <- arr[q]                    // 以 [p , q] 区域中最后一个元素作为中间值
    while true：                       // 一直循环，直到执行 end while
        while arr[lo] < pivot:         // lo 从左往右遍历，直至找到一个不小于 pivot 的元素
            lo <- lo+1
        while hi>0 and arr[hi] > pivot:   // hi 从右往左遍历，直至找到一个不小于 pivot 的元素
            hi <- hi-1
        if lo ≥ hi:                      // 如果 lo 大于等于 hi，退出循环
            end while
        else:
            swap arr[lo] , arr[hi]        // 交换 arr[lo] 和 arr[hi] 的值
            lo <- lo+1                    // 分别将 lo 和 hi 向前移动一步，准备遍历后续的元素
            hi <- hi-1
    swap arr[lo] , arr[q]                 // 跳出循环后，交换 arr[lo] 和 arr[q] 的值
    return lo                             // 返回 lo 的值，也就是中间值所在序列中的位置

快速排序算法的实现

结合伪代码，如下是用快速排序算法对 {35, 33, 42, 10, 14, 19, 27, 44, 26, 31} 完成升序排序的 C 语言程序：

#include <stdio.h>
// arr 为待排序数组，[p,q] 用于指定排序区域
int partition(int* arr, int p, int q) {
    int temp = 0;
    // lo、hi分别表示指向首个元素和倒数第 2 个元素的指针
    int lo = p;
    int hi = q - 1;
    //pivot 表示选中的中间值
    int pivot = arr[q];
    while (1)
    {
        //lo从左往右遍历，直至找到一个不小于 pivot 的元素
        while (arr[lo] < pivot) {
            lo++;
        };
        //hi从右往左遍历，直至找到一个不大于 pivot 的元素
        while (hi > 0 && arr[hi] > pivot) {
            hi--;
        }
        //如果 lo≥hi，退出循环
        if (lo >= hi)
        {
            break;
        }
        else {
            //交换 arr[lo] 和 arr[hi] 的值
            temp = arr[lo];
            arr[lo] = arr[hi];
            arr[hi] = temp;
            // lo 和 hi 都向前移动一个位置，准备继续遍历
            lo++;
            hi--;
        }
    }
    //交换 arr[lo] 和 arr[q] 的值
    temp = arr[lo];
    arr[lo] = pivot;
    arr[q] = temp;
    //返回中间值所在序列中的位置
    return lo;
}

void quick_sort(int* arr, int p, int q) {
    int par;
    //如果待排序序列不存在，或者仅包含 1 个元素，则不再进行分割
    if (q - p <= 0) {
        return;
    }
    else {
        //调用 partition() 函数，分割 [p,q] 区域
        par = partition(arr, p, q);
        //以 [p,par-1]作为新的待排序序列，继续分割
        quick_sort(arr, p, par - 1);
        //以[par+1,q]作为新的待排序序列，继续分割
        quick_sort(arr, par + 1, q);
    }
}

int main()
{
    int i = 0;
    int arr[10] = { 35,33,42,10,14,19,27,44,26,31 };
    //对于 arr 数组中所有元素进行快速排序
    quick_sort(arr, 0, 9);
    for (; i < 10; i++) {
        printf("%d ", arr[i]);
    }
    return 0;
}

如下是用快速排序算法对 {35, 33, 42, 10, 14, 19, 27, 44, 26, 31} 完成升序排序的 Java 程序：

public class Demo {
    public static int partition(int[] arr, int p, int q) {
        int temp = 0;
        // lo、hi分别表示指向首个元素和倒数第 2 个元素的指针
        int lo = p;
        int hi = q - 1;
        // pivot 表示选中的中间值
        int pivot = arr[q];
        while (true) {
            // lo从左往右遍历，直至找到一个不小于 pivot 的元素
            while (arr[lo] < pivot) {
                lo++;
            }
            // hi从右往左遍历，直至找到一个不大于 pivot 的元素
            while (hi > 0 && arr[hi] > pivot) {
                hi--;
            }
            // 如果 lo≥hi，退出循环
            if (lo >= hi) {
                break;
            } else {
                // 交换 arr[lo] 和 arr[hi] 的值
                temp = arr[lo];
                arr[lo] = arr[hi];
                arr[hi] = temp;
                // lo 和 hi 都向前移动一个位置，准备继续遍历
                lo++;
                hi--;
            }
        }
        // 交换 arr[lo] 和 arr[q] 的值
        temp = arr[lo];
        arr[lo] = pivot;
        arr[q] = temp;
        // 返回中间值所在序列中的位置
        return lo;
    }

    public static void quick_sort(int[] arr, int p, int q) {
        //如果待排序序列不存在，或者仅包含 1 个元素，则不再进行分割
        if (q - p <= 0) {
            return;
        } else {
            //调用 partition() 函数，分割 [p,q] 区域
            int par = partition(arr, p, q);
            //以 [p,par-1]作为新的待排序序列，继续分割
            quick_sort(arr, p, par - 1);
            //以[par+1,q]作为新的待排序序列，继续分割
            quick_sort(arr, par + 1, q);
        }
    }

    public static void main(String[] args) {
        int[] arr = new int[] { 35, 33, 42, 10, 14, 19, 27, 44, 26, 31 };
        // 对于 arr 数组中所有元素进行快速排序
        quick_sort(arr, 0, 9);
        for (int i = 0; i < arr.length; i++) {
            System.out.print(arr[i]+" ");
        }
    }
}

如下是用快速排序算法对 {35, 33, 42, 10, 14, 19, 27, 44, 26, 31} 完成升序排序的 Python 程序：

def partition(arr,p,q):
    #lo、hi分别表示指向首个元素和倒数第 2 个元素的索引
    lo = p
    hi = q-1
    #pivot 表示选中的中间值
    pivot = arr[q]
    while True:
        #lo从左往右遍历，直至找到一个不小于 pivot 的元素
        while arr[lo] < pivot:
            lo = lo + 1
        #hi从右往左遍历，直至找到一个不大于 pivot 的元素
        while hi > 0 and arr[hi] > pivot:
            hi = hi - 1
        #如果 lo≥hi，退出循环
        if lo >= hi:
            break
        else:
            #交换 arr[lo] 和 arr[hi] 的值
            arr[lo],arr[hi] = arr[hi],arr[lo]
            #lo 和 hi 都向前移动一个位置，准备继续遍历
            lo = lo + 1
            hi = hi - 1
    #交换 arr[lo] 和 arr[q] 的值
    arr[lo],arr[q] = arr[q],arr[lo]
    #返回中间值所在序列中的位置
    return lo

def quick_sort(arr,p,q):
    #如果待排序序列不存在，或者仅包含 1 个元素，则不再进行分割
    if q - p <= 0:
        return
    #调用 partition() 函数，分割 [p,q] 区域
    par = partition(arr,p,q)
    #以 [p,par-1]作为新的待排序序列，继续分割
    quick_sort(arr,p,par-1)
    #以[par+1,q]作为新的待排序序列，继续分割
    quick_sort(arr,par+1,q)
  
arr=[35,33,42,10,14,19,27,44,26,31]
#对于 arr 列表中所有元素进行快速排序
quick_sort(arr,0,9)
print(arr)

以上程序的输出结果均为：

10 14 19 26 27 31 33 35 42 44

本文链接：http://task.lmcjl.com/news/12591.html