百钱买百鸡Python编程详解

关键词

百钱买百鸡Python编程详解

中国古代数学家张丘建在他的《算经》中提出了一个著名的“百钱百鸡问题”：一只公鸡值五钱，一只母鸡值三钱，三只小鸡值一钱，现在要用百钱买百鸡，请问公鸡、母鸡、小鸡各多少只？

问题分析

用百钱如果只买公鸡，最多可以买 20 只，但题目要求买 100 只，由此可知，所买公鸡的数量肯定在 0～20 之间。同理，母鸡的数量在 0～33 之间。在此不妨把公鸡、母鸡和小鸡的数量分别设为 cock、hen、chicken，则 cock+hen+chicken=100，因此百钱买百鸡问题就转化成解不定方程组的问题了。

算法设计

对于不定方程组，我们可以利用穷举循环的方法来解决，也就是通过对未知数可变范围的穷举，验证方程在什么情况下成立，从而得到相应的解。

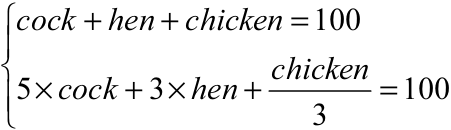
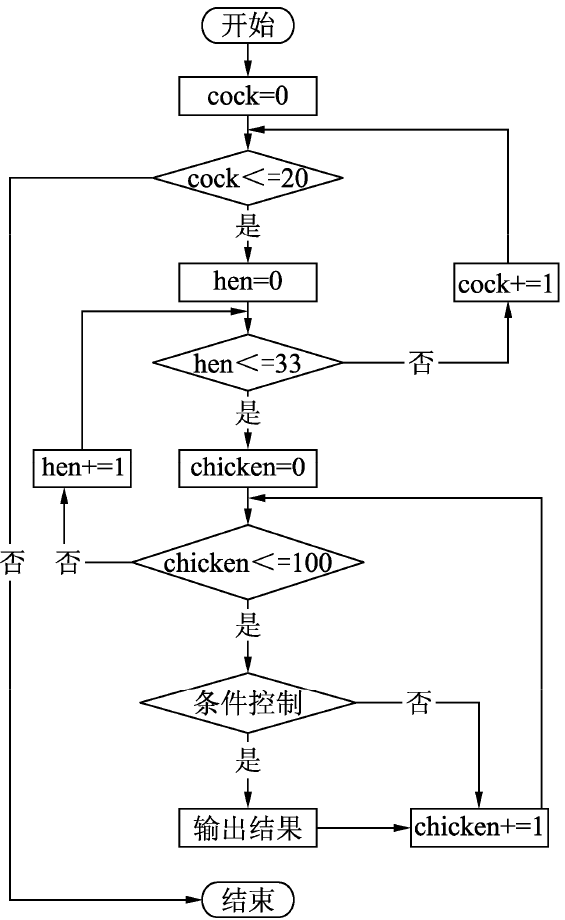
因公鸡的取值范围是 0~20，可用循环语句for cock in range(0,21)实现。钱的数量是固定的，要买的鸡的数量也是固定的，所以母鸡数量是受到公鸡数量限制的。同理，小鸡数量受到公鸡和母鸡数量的限制，因此我们可以利用三层循环的嵌套来解决，第一层循环控制公鸡的数量，第二层控制母鸡的数量，最内层控制小鸡的数量。

确定程序框架

在设计循环时首先要考虑循环的三要素，即循环变量的初值、循环的控制条件和使循环趋于结束的循环变量值的改变。

针对本题来说，每层循环的初值是 0（即买的 100 只鸡中，可能没有公鸡，也可能没有母鸡或小鸡），循环的控制条件是公鸡、母鸡和小鸡用百钱最多能够买到的数量（公鸡最多 20 只，母鸡最多 33 只，小鸡最多 100 只，虽然百钱最多可以买到 300 只小鸡，但题目要求只买100只）。穷举循环的特点就是把所有情况都考虑到，因此每层循环执行一次，对应循环变量的值就要加1。

程序流程图如下图所示：

根据流程图，构建程序框架如下：

cock = 0
while cock <= 20:
    # 内层循环控制母鸡数量取值范围为0~33
    hen = 0
    while hen <= 33:
        #内层循环控制小鸡数量取值范围为0~100
        chicken = 0
        while chicken <= 100:
            #条件控制
            print("cock=%2d,hen=%2d,chicken=%2d\n" %(cock,hen,chicken))
            chicken += 1
        hen += 1
    cock += 1

根据这三层循环，我们可以得到很多种方案，在这些方案中有些是不符合 cock+hen+chicken=100 并且 5×cock+3×hen+chicken/3=100 这两个条件的。

因此结果输出之前，我们要把合理的方案筛选出来，即如果结果满足 cock+hen+chicken=100 和 5×cock+3×hen+chicken/3=100，则输出。很明显，控制条件即为语句 if(5×cock+3×hen+chicken/3.0==100)and(cock+hen+chicken==100)。

完整的程序

根据上面的分析，编写程序如下：

if __name__=="__main__":
    # cock表示公鸡数量，hen表示母鸡数量，chicken表示小鸡数量，总共100只
    # 外层循环控制公鸡数量取值范围为0~20
    cock = 0
    while cock <= 20:
        # 内层循环控制母鸡数量取值范围为0~33
        hen = 0
        while hen <= 33:
            #内层循环控制小鸡数量取值范围为0~100
            chicken = 0
            while chicken <= 100:
                # 条件控制
                if (5 * cock + 3 * hen + chicken / 3.0 ==100) and (cock + hen + chicken ==100):
                    print("cock=%2d,hen=%2d,chicken=%2d" %(cock,hen,chicken))
                chicken += 1
            hen += 1
        cock += 1

程序的运行结果为：

cock= 0,hen=25,chicken=75
cock= 4,hen=18,chicken=78
cock= 8,hen=11,chicken=81
cock=12,hen= 4,chicken=84

更高效的程序

以上算法需要穷举尝试 21×34×101=72114 次，算法的效率显然太低了。对于这类求解不定方程的问题，各层循环的控制变量直接与方程的未知数相关，并且采用对未知数的取值范围穷举和组合的方法得到全部的解。

对于本题来说，公鸡的数量确定后，小鸡的数量就固定为 100-cock-hen，无须再进行穷举了，此时约束条件只有一个，即 5×cock+3×hen+chicken/3=100，这样我们利用两重循环即可求解本题，代码如下：

if __name__=="__main__":
    # 外层循环控制公鸡数量取整范围为0～20
    cock = 0
    while cock <= 20:
        # 内层循环控制母鸡数量取值范围为0～30
        hen = 0
        while hen <= 33:
            # 小鸡的数量
            chicken = 100 - cock - hen
            if 5 * cock + 3 * hen + chicken / 3.0 == 100:
                print("cock=%2d,hen=%2d,chicken=%2d" %(cock, hen, chicken))
            hen+=1
        cock+=1

程序的运行结果为：

cock= 0,hen=25,chicken=75
cock= 4,hen=18,chicken=78
cock= 8,hen=11,chicken=81
cock=12,hen= 4,chicken=84

此算法只需穷举 21×34=714 次，实现时约束条件又限定 chicken 能被 3 整除时才会判断“5×cock+3×hen+chicken/3.0=100”，这样便省去了 chicken 不能整除 3 时的算术计算和条件判断，进一步提高了算法的效率。

本文链接：http://task.lmcjl.com/news/15230.html

展开阅读全文

上一篇：Python os.tcgetpgrp() 方法详解下一篇：详解Python os.pipe2（进程间通信管道）使用方法

热门文章排行

推荐文章

关键词

百钱买百鸡Python编程详解

问题分析

算法设计

确定程序框架

完整的程序

更高效的程序