目录
\[H(X)=-\sum_{i=1}^{n}P(X=i)log_{2}P(X=i)
\]
\[H(X|Y)=-\sum_{v\in values(Y)}P(Y=v)H(X|Y=v) \\
H(X|Y=v)=-\sum_{i=1}^{n}P(X=i|Y=v)log_{2}P(X=i|y=v)
\]
\[I(X,Y)=H(X)-H(X|Y)=H(Y)-H(Y|X)
\]
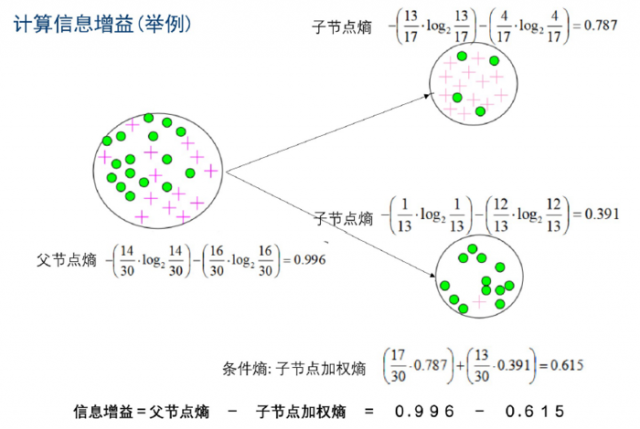
我们通常会选择信息增益最大的作为分割特征。

| Outlook | Temperature | Humidity | Windy | PlayGoIf? |
|---|---|---|---|---|
| sunny | 85 | 85 | FALSE | no |
| sunny | 80 | 90 | TRUE | no |
| overcast | 83 | 86 | FALSE | yes |
| rainy | 70 | 96 | FALSE | yes |
| rainy | 68 | 80 | FALSE | yes |
| rainy | 65 | 70 | TRUE | no |
| overcast | 64 | 65 | TRUE | yes |
| sunny | 72 | 95 | FALSE | no |
| sunny | 69 | 70 | FALSE | yes |
| rainy | 75 | 80 | FALSE | yes |
| sunny | 75 | 70 | TRUE | yes |
| overcast | 72 | 90 | TRUE | yes |
| overcast | 81 | 75 | FALSE | yes |
| rainy | 71 | 95 | TRUE | no |
将Temperature按如下规格分为三类:
HOT:[80-90)
Middle:[70,80)
Cool:[60,70)
(很显然这里的温度用的不是摄氏度)
将湿度按如下规格分为两类:
High:>=85
Normal: <85
选择Play Golf为父节点,那么
| PlayGoIf? | Frequency | P | Entropy |
|---|---|---|---|
| Yes | 5 | 0.36 | -0.531 |
| No | 9 | 0.64 | -0.410 |
| 14 | 0.940 |
其中,比如Yes的概率,就是根据上面的公式算出来的:
\[E(Yes)=0.36\times log_{2}{0.36}\approx -0.531 \\
E(No)=0.64\times log_{2}{0.64}\approx -0.410 \\
H(X)=-E(Yes)-E(No)=0.940 \\
\]
按不同字段分割,计算结果如下: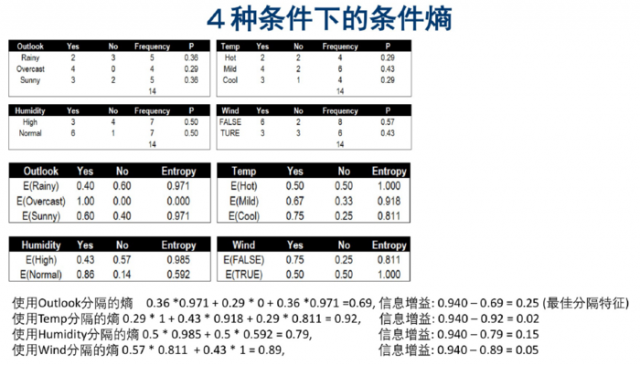
计算决策树特征重要性的步骤:
假设数据有M个特征,使用信息熵来决定每一个分叉的情况:
同时训练多个决策树,预测的时候,综合考虑多个结果预测.例如取多个结果的均值,众数
本文链接:http://task.lmcjl.com/news/726.html