本文介绍了Explainable ML(可解释性的机器学习)的相关内容，抱愧这项技术的相关概述、当前发展等等。

在前面的学习之中，我们已经学习了很多的模型，它能够针对特定的任务，接受我们的输入并产生目标的输出。但我们并不满足于此，我们甚至希望机器告诉我们，它是如何得到这个答案的，而这就是可解释的机器学习。

Why we need Explainable ML

首先我们要明确，即使我们训练出来的模型能够得到一个正确的输出，但是这并不代表它真正学习到了内核的规律所在，因此我们总是希望能够知道为什么机器给出这个答案，在一些特定的场景也是如此：

• 例如将机器学习用于医疗诊断，那我们希望机器做出来的决策是有根据的
• 将机器学习用于法律，那我们也希望看到机器学习做出判定背后的原因，是否存在歧视问题等

而且如果我们能够拥有可解释性的机器学习，那么在模型的效果不好的时候，我们便能够知道是哪部分出现了问题，可直接调整解决。

而对于可解释性的机器学习，它的评价标准来说一直很难定夺，因为一个理由的可解释是因人而异的。

可解释性VSPowerful

对比一下线性模型、深度学习网络、决策树这三个模型的特点：

• 线性模型的可解释性比较强，我们能够通过各个权重和偏置来简单地理解线性模型之间各个变量的关系；但是线性模型其拟合未知函数的能力较弱
• 深度学习网络的能力很强大，能够完成非常多复杂的任务，但是它的可解释性比较差， 我们很难理解其内部的含义
• 单颗决策树的可解释性很强，并且决策森林的拟合能力也是很好的。但是如果决策森林中决策树的数目很多的话，其可解释性也一样会变差

因此并没有模型能够简单地完美解决拟合能力和可解释性的问题

Explainable ML

假设模型是根据一张图片做出其所属的分类，那么可解释性的机器学习大致可以分为两大类：

• Local Explanation：它要回答的问题是机器为什么会觉得这张图片是属于这一类
• Global Explanation：它要回答的问题是你觉得这一类的图片应该长什么样子，这个类别的模型比较特殊，没有针对某张图片而是针对整个类。

Local Explanation:Explain the Decision

这个类别的模型，我们可以把问题转换成更具体一点：是输入中的哪一个部分让机器觉得它属于这个类别呢？例如对于输入x来说可以写成多个组成部分\(\{x_1,...,x_n,...,x_N\}\)，例如在图片中每一个就代表一个像素，在句子中每一个就代表一个词汇等等。那么如果我们希望找到哪个对结果影响最大的组成部分，可行的办法是逐个改变或删除组成部分，看看在改变哪一个的时候机器的输出会发生变化，例如下图的例子：

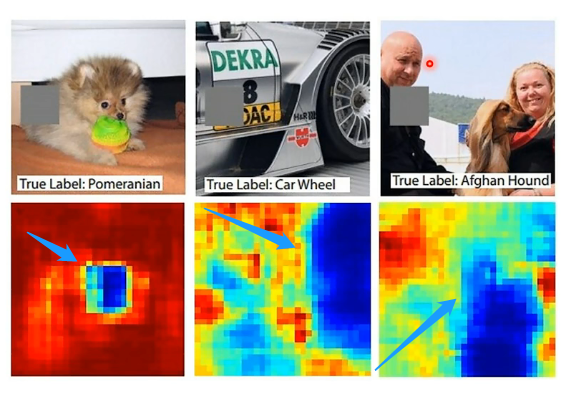
上面代表在每一张图片中使用一个灰色方块去不断遮挡某一部分，当遮挡到蓝色部分的时候就会发现机器无法做出正确预测。

那么还有一个更进阶的想法叫做Saliency Map，即将输入表示成一个向量\(\{x_1,...,x_n,...,x_N\}\)，那么该输入对应的输出与真正的输出之间就可以计算损失Loss。那么具体的想法就是不断尝试改变每一个分量的值为\(x_n=x_n+\Delta x\)，那么相应的Loss也变化，因此我们可以从Loss变换的程度来看这个变量对于结果的影响性有多大，即：

\[\vert \frac{\Delta L}{\Delta x_n} \vert=\vert \frac{\partial L}{\partial x_n}\vert
\]

相当于梯度的值越大，该值对于结果的影响力就越大，该变量就越重要，如下图：

但这个方法也存在一定的局限性， 或者说在某些场景中表现也不是很好，例如下图的中间图片，虽然它将羚羊的大致轮廓表达了出来，但是另外区域的杂讯还是特别的多；因此我们可以用SmoothGrad来尝试解决，得到右边的图，可以看到效果更好：

那么SmoothGrad的做法是为原始的图片重复多次，每次加入随机产生的杂讯来影响每一个像素点，然后对于每一次得到的图像都画Saliency Map，最后再将其平均起来即可。

而上述的通过梯度计算然后画出对应Saliency Map的方法也存在一定的局限性，就是在梯度上产生了问题，例如下面的例子为某种生物鼻子的长度的变化所引起该生物是否是大象的概率的变化：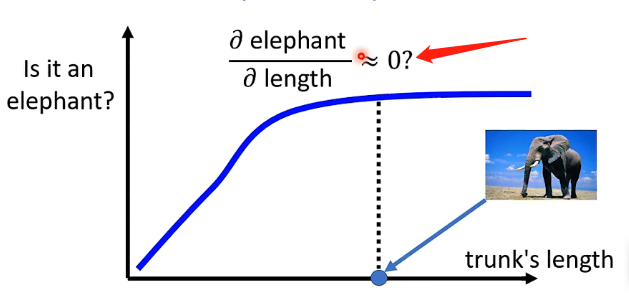

可以看到在鼻子长度较大的点处，此处因为是大象的概率已经很高了，因此其梯度很小，那我们如果直接计算其梯度的话就会得到结果说鼻子的长度对是否是大象的概率没有影响，这显然是不符合逻辑的！

那么还有另外一个能够认识到模型各个模块相关功能的办法，具体可以用一个语音辨认的例子来解释：假设我们当前的语音辨识模型有很多层，那我们训练一个模型将向量转换为语音的输出，那么就可以对每一层输出的Embedding都放入这个转换为语音的模型中得到输出，我们再听每一层对应的语音输出，就可以明确每一层对声音的处理起到了什么作用。

Global Explaination:Explain the Whole Model

对于这个类别的可解释性模型来说，它并不是告诉我们一个特定的样本长什么样子、属于什么分类，而是根据模型内的参数来理解说为什么某一个类的样本会长这个样子，可以简单理解为我们要机器告诉我们它心理想象的猫长什么样子。

下面通过一个图像检测的例子来说明我们对于这种问题的解决思路。

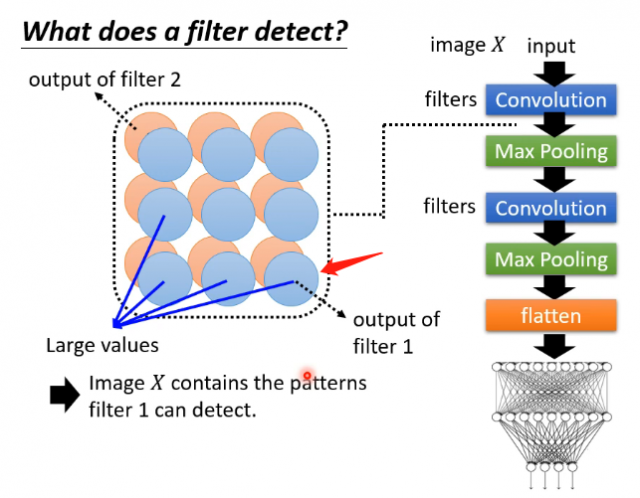
对于图中的每一个filter，可以看成它是对上一层所输出的图像的某一块区域的监测，如果监测到它希望得到的信息，那么它的值就会比较大。但是现在Global Explaination的任务不是针对特定样本而言，也就是说我们没有样本来生成各层的图像。而为了知道每一层的每一个filter它想要监测什么内容，我们可以来创造图像，即如上图所示，我们创造一个图片对应的向量，使得它输出进入能够使得我们当前观察的这个filter最大，即

\[X^*=argmax_X \sum_i\sum_j a_{ij}
\]

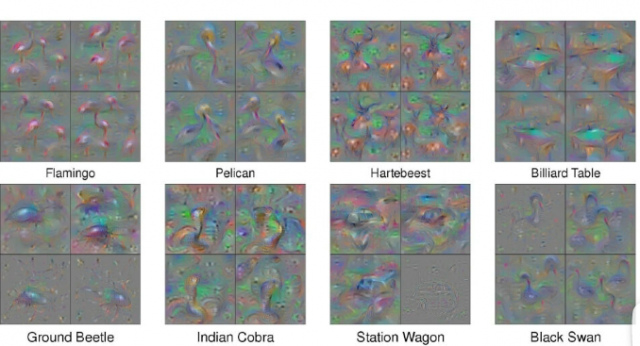
那么我们再来观测\(X^*\)对应的图像，我们就可以知道这个filter它想检测什么样的类型了，如下图：

例如上图就有的filter检测横条纹、竖条纹等等等等。

那么上述的思路，我们能否将其直接用于输出层呢？例如我们直接让：

\[X^*=argmax_X~y_i
\]

也就是说我们找一张图片，让这个图片通过机器后输出某一个类别的概率最大，那么有可能实现吗？实际上效果很差！例如在手写数字的识别例子中：

为什么会这样呢？这其中的解释大概可以说成：因为机器它不一定是看到某个数字的样子才会输出对应的类别，它可能真的没有学习到这个规律，只是学习到从一堆杂讯中寻找到它认为是某个类别的信息。那么如果真的要用这个方法，需要根据我们对于图像的深层次理解加上一大堆的假设，并且好好调整参数才可能得到，如下图：

那么为了避开上述这么多的约束呢，我们还有一个办法就是引入生成器来帮助。即我们假设已经通过很多的图片训练完成了一个生成器（用GAN、VAE等），然后我们将生成器接到原分类模型之前，即：

那现在我们的目标就转换成：

\[z^*=argmax_z ~y_i
\]

即找到一个z的向量，生成图片之后能够使得y对该图片的分类的信心分数最大。那么我们要得到可解释性的东西，就再将向量\(z^*\)转换成图片即可，即：

\[X^*=G(z^*)
\]

这样得到的效果可能是很好的。