1. 一些基本概念

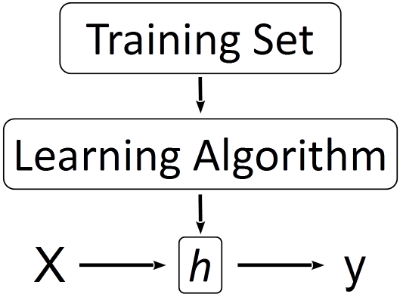
图1. 机器学习的基本过程

• 训练集（Training Set）：为了研究一个变量（x）与另一个变量（y）的关系，而通过观察、测量等方式获得的一组数据。这组数据中收集了x和与之对应的y——一个数据对（x, y）。例如我们要研究房屋面积（x）和售价（y）之间的关系，每观察一套已出售的房屋，就得到一个数据对（x, y）。观察10套已出售的房屋，就可以得到10个这样的数据对，这时就得到了一个用来研究房屋面积和售价之间的关系的训练集了（虽然样本量比较小）。这些数据集一般采集自现实环境中，属于现象（我们的目的是透过现象看本质）。

• 样本（Sample）：训练集中采集数据的对象就是一个样本，例如一套已出售的房屋。

• 模型（Model）：由于某些历史原因，机器学习中的模型也被叫做假设（hypothesis, h），这个h就是我们透过现象想要寻找的"本质"。建立模型的过程通常就是确定一个函数表达式的过程（是否还记得寒假作业中的这类题目：观察一组数，写出下一个数是什么？）。最常见的模型是回归模型（线性回归或逻辑回归等），例如我们假设房屋面积与售价之间的关系是一个线性回归模型，则可以写成：

  h(θ)=θ0+θ1x…(1)h(θ)=θ0+θ1x…(1)

  其中h是函数（可能更习惯叫做y，但在机器学习中y一般表示已知的函数值，即后面的因变量；这里的h相当于预测得到的y），θ是函数的参数（也可以看做是每个自变量的权重，权重越大，对y的影响也越大），x是自变量。

• 训练模型（Training Model）：选定模型（选择合适的模型需要丰富的经验）后，函数的一般形式就确定了。通常所说的训练模型是指利用训练集求解函数的待定参数的过程。上面的(1)式与直线方程的一般形式y = ax + b是相同的，这里不过换了一种写法。此时我们知道模型是一条直线，为了确定这条直线的确定方程，我们需要求出两个未知的参数——θ₀（截距）和θ₁（斜率），如果训练集中只有两个样本，那就只是求一个二元二次方程组就解决问题了。

• 特征（Feature）：特征就是在一个模型中，所有想研究的自变量（x）的集合。例如我们在研究房屋售价的模型中，所有可能影响售价的因素都可以看成是一个特征，房屋面积、所在城市、房间个数等。在建立模型的过程中，特征的选择是一个大学问，甚至有专门的分支来研究特征选择或特征表示。

2. 训练集的表示

上面提到过，训练集就是许多的（x, y）数据对的集合。其中x是因变量，y是自变量。通常认为x的变化引起了y的改变，即x的值决定了y的值。在预测房屋价格的模型中，假如我们能找到所有影响房屋价格的因素（所有的x），并且确定各个因素准确的参数（θ），那么理论上可以准确的预测出任何房屋的价格（y）。

2.1 单因素训练集中自变量的表示方法

• 单因素相当于方程中只有一个自变量，这个自变量可以用一个小写字母x来表示；
• 如果收集了多个样本，则通过在右上角添加带括号的角标的方式区分，表示为x⁽¹⁾, x⁽²⁾, ..., x^(m)，其中m表示样本的个数；
• 矩阵的表示：向量一般用小写字母表示，矩阵用大写字母表示。所有单因素样本中的x可以用一个m x 1（m行1列）的列向量x(小写字母)（只有一列的矩阵就是一个列向量）来表示：

  x=⎛⎝⎜⎜⎜⎜⎜x(1)x(2)⋮x(m)⎞⎠⎟⎟⎟⎟⎟x=(x(1)x(2)⋮x(m))

2.2 多因素训练集中自变量的表示方法

• 多因素相当于方程中有多个自变量（多个feature），不同的自变量之间使用右下角添加不带括号的角标来区分，表示为x₁, x₂, ..., x_n，其中n表示feature的个数；
• 当存在多个样本时，可以用一个m x n（m行n列）的矩阵X(大写字母)来表示：

  X=⎡⎣⎢⎢⎢⎢⎢⎢⎢x(1)1x(2)1⋮x(m)1x(1)2x(2)2⋮x(m)2……⋱…x(1)nx(2)n⋮x(m)n⎤⎦⎥⎥⎥⎥⎥⎥⎥X=[x1(1)x2(1)…xn(1)x1(2)x2(2)…xn(2)⋮⋮⋱⋮x1(m)x2(m)…xn(m)]

2.3 训练集中因变量的表示方法

无论是单因素还是多因素，每一个样本中都只包含一个因变量（y），因此只需要区分不同样本间的y，y⁽¹⁾, y⁽²⁾, ..., y^(m)，其中m表示样本的个数；

用列向量y表示为：

y=⎛⎝⎜⎜⎜⎜⎜y(1)y(2)⋮y(m)⎞⎠⎟⎟⎟⎟⎟y=(y(1)y(2)⋮y(m))

3. 参数的表示

也许是某种约定，在机器学习中，一般都是用θ来表示参数，参数是自变量X的参数（也可以看做是每个自变量的权重，权重越大的自变量对y的影响也越大），理论上，有多少个自变量就有多少个参数，但就像在直线方程y = ax + b中表现出来的那样，除了x的参数a，还有一个常数项b。因此参数一般比自变量的个数多一个，当有n个自变量的时候，会有n+1个参数。

最终的模型是由一个特定的方程来表示的，在训练模型的过程中，确定了这个方程中的未知参数。这些参数对于所有的样本都是相同的，例如第一个样本x⁽¹⁾中的第一个自变量x₁的参数与任意其他样本x⁽ⁱ⁾中第一个自变量x₁的参数是相同的。因此不用区分样本间的参数，只用区分不同自变量之间的参数，可以使用一个n+1维的列向量θ来表示所有的参数：

θ=⎛⎝⎜⎜⎜⎜θ0θ1⋮θn⎞⎠⎟⎟⎟⎟θ=(θ0θ1⋮θn)

4. 模型的表示

这里说的模型就是一个特定的函数，上面已经提过，模型一般使用h来表示。下面用线性回归模型来举例说明模型的符号表示。

4.1 直接表示

直接表示方法是我们在没有学习线性代数之前的代数表示方式。

• 单变量线性回归方程：

  hθ(x)=θ0+θ1xhθ(x)=θ0+θ1x

• 多变量线性回归方程：

  hθ(x)=θ0+θ1x1+θ2x2+θ3x3+…+θnxnhθ(x)=θ0+θ1x1+θ2x2+θ3x3+…+θnxn

4.2 矩阵表示

学习了线性代数后，可以使用矩阵来表示上面的方程，不仅表示起来方便，直接进行矩阵运算效率也更高效。在这里需要特别说明的一点是，为了配合矩阵的表示，在上面的方程中添加了x₀，并且x₀=1，且将θ₀作为x₀的参数。

• 单变量/多变量线性回归方程：

  hθ(x)=Xθ=⎡⎣⎢⎢⎢⎢⎢⎢⎢x(1)0x(2)0⋮x(m)0x(1)1x(2)1⋮x(m)1……⋱…x(1)nx(2)n⋮x(m)n⎤⎦⎥⎥⎥⎥⎥⎥⎥⎡⎣⎢⎢⎢⎢θ0θ1⋮θn⎤⎦⎥⎥⎥⎥hθ(x)=Xθ=[x0(1)x1(1)…xn(1)x0(2)x1(2)…xn(2)⋮⋮⋱⋮x0(m)x1(m)…xn(m)][θ0θ1⋮θn]

  ，此时X是一个m x (n+1)的矩阵，每一行表示一个样本，每一列表示一个特征，结果是一个m x 1的列向量，其中m表示样本的个数，n表示变量的个数（X中的每一列具有同样的参数，一列表示在不同的样本中同一个特征的取值）；

• 当只有一个样本多个变量时，还可以表示为：

  hθ(x)=θTx=[θ0θ1…θn]⎡⎣⎢⎢⎢⎢x0x1⋮xn⎤⎦⎥⎥⎥⎥hθ(x)=θTx=[θ0θ1…θn][x0x1⋮xn]

  ，此时x是一个(n+1)维的列向量，每一行表示一个变量的值。

参考：https://www.coursera.org/learn/machine-learning