计算训练误差和泛化误差可以使用之前介绍过的损失函数,例如线性回归用到的平方损失函数和softmax回归用到的交叉熵损失函数。
机器学习模型应关注降低泛化误差。
在实践中,我们要尽可能同时应对欠拟合和过拟合。虽然有很多因素可能导致这两种拟合问题,这里主要讨论两个因素:模型复杂度和训练数据集大小。
以多项式函数拟合为例。给定一个由标量数据特征和对应的标量标签组成的训练数据集,多项式函数拟合的目标是找一个k阶多项式函数
来近似y,w(k)是模型的权重参数,b是偏差参数。与线性回归相同,多项式函数拟合也使用平方损失函数。特别地,一阶多项式函数拟合又叫线性函数拟合。
给定训练数据集,模型复杂度和误差之间的关系: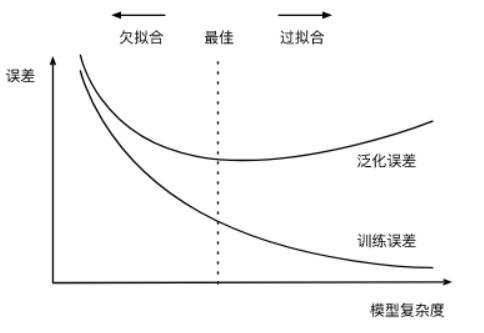
一般来说,如果训练数据集中样本数过少,特别是比模型参数数量(按元素计)更少时,过拟合更容易发生。此外,泛化误差不会随训练数据集里样本数量增加而增大。
因此,在计算资源允许的范围之内,我们通常希望训练数据集大一些。特别是在模型复杂度较高时,例如层数较多的深度学习模型。
在西瓜书中介绍了三种划分数据集的方法:留出法、交叉验证法和自助法。
方法:在模型原损失函数基础上添加L2范数惩罚项
权重衰减等价于L2范数正则化(regularization)。通过惩罚绝对值较大的模型参数应对过拟合。
L2范数正则化在模型原损失函数基础上添加L2范数惩罚项,从而得到训练所需要最小化的函数。L2范数惩罚项指的是模型权重参数每个元素的平方和与一个正的常数的乘积
以线性回归中的线性回归损失函数为例,线性回归的原损失函数: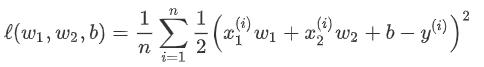
将权重参数用向量W=[w₁,w₂]表示,带有L2范数惩罚项的新损失函数为:
其中向量L2范数|w|²平方展开后得到w₁²+w₂²。
λ>0,且当λ较大时,惩罚项在损失函数中的比重较大,这通常会使学到的权重参数的元素较接近0。当λ设为0时,惩罚项完全不起作用。
新的优化函数为: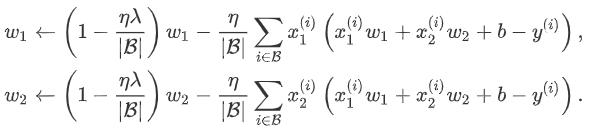
方法:以一定的概率丢弃使用该方法的某层的某个单元
当对一个隐藏层使用丢弃法时,该层的隐藏单元将有一定概率被丢弃掉。设丢弃概率为p,那么有p的概率hᵢ会被清零,有1-p的概率hᵢ会除以1-p做拉伸。
丢弃某些单元后,新的隐藏层单元为:
丢弃法不改变其输入的期望值。
丢弃后的神经网络示意图: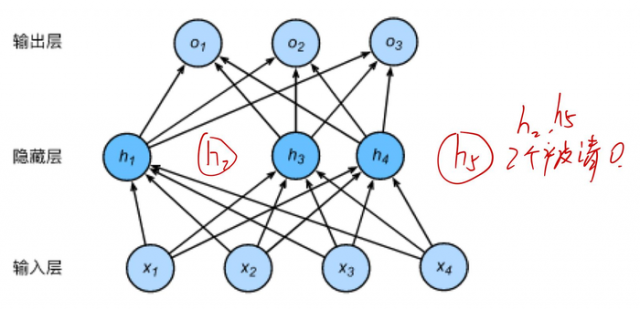
当神经网络的层数较多时,模型的数值稳定性容易变差。即容易产生梯度消失和梯度爆炸。
深度模型有关数值稳定性的典型问题是消失(vanishing)和爆炸(explosion)。

假设输出层只有一个输出单元,且隐藏层使用相同的**函数。如果将每个隐藏单元的参数都初始化为相等的值,那么在正向传播时每个隐藏单元将根据相同的输入计算出相同的值,并传递至输出层。在反向传播中,每个隐藏单元的参数梯度值相等。因此,这些参数在使用基于梯度的优化算法迭代后值依然相等。之后的迭代也是如此。在这种情况下,无论隐藏单元有多少,隐藏层本质上只有1个隐藏单元在发挥作用。
因此,通常将神经网络的模型参数,特别是权重参数,进行随机初始化
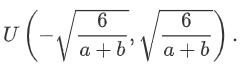
输入变,输出不变
协变量变化问题的根源在于特征分布的变化(即协变量的变化),输入的分布可能随时间而改变,但是标记函数,即条件分布P(y∣x)不会改变。
输入不变,输出变
标签P(y)上的边缘分布的变化,但类条件分布是不变的P(x∣y)。
病因(要预测的诊断结果)导致 症状(观察到的结果),即y导致x。
标签含义发生变化
如南北方人关于“饭”的定义。
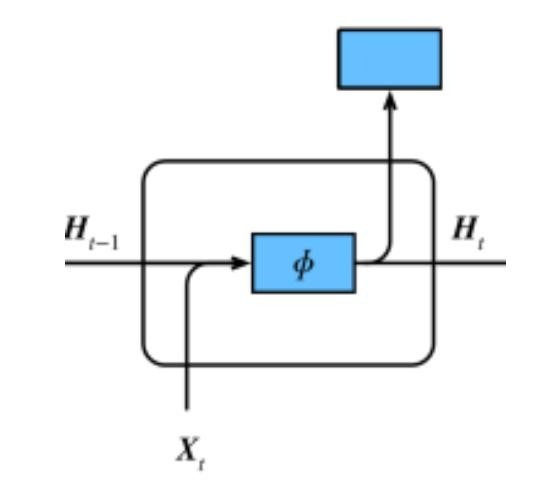
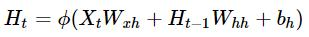
门控循环神经网络(Gate Recurrent Unit),捕捉时间序列中时间步距离较⼤的依赖关系。
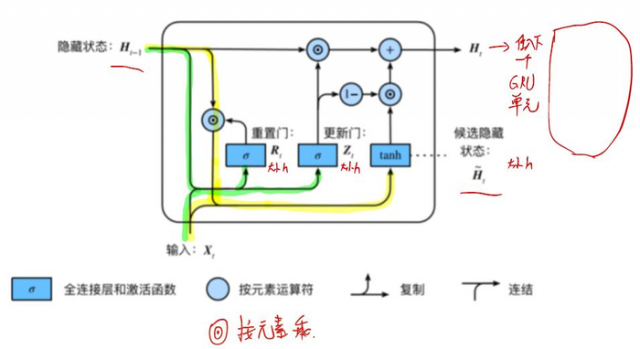
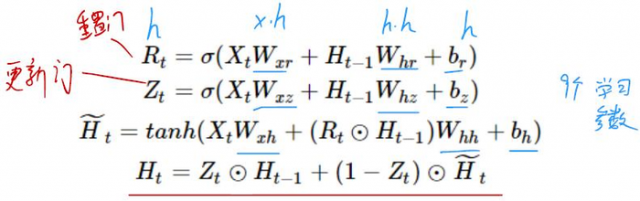
• 重置⻔有助于捕捉时间序列⾥短期的依赖关系;
• 更新⻔有助于捕捉时间序列⾥⻓期的依赖关系。
长短期记忆long short-term memory
遗忘门:控制上一时间步的记忆细胞
输入门:控制当前时间步的输入
输出门:控制从记忆细胞到隐藏状态
记忆细胞:⼀种特殊的隐藏状态的信息的流动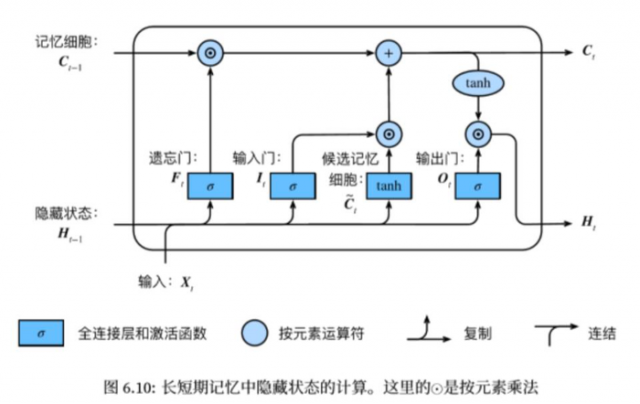
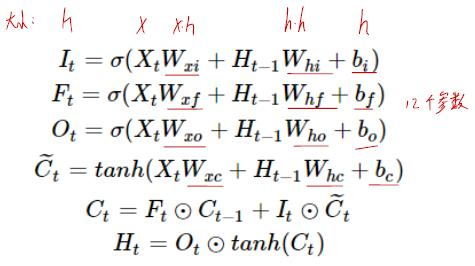
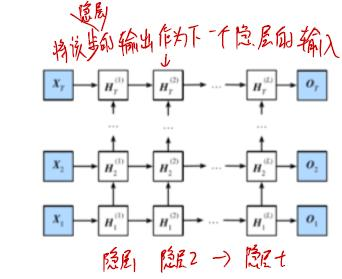
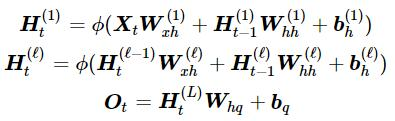
深度循环神经网络并不是深度越深越好
由于双向关联,所以非常常用,但也并非所有都适合该网络。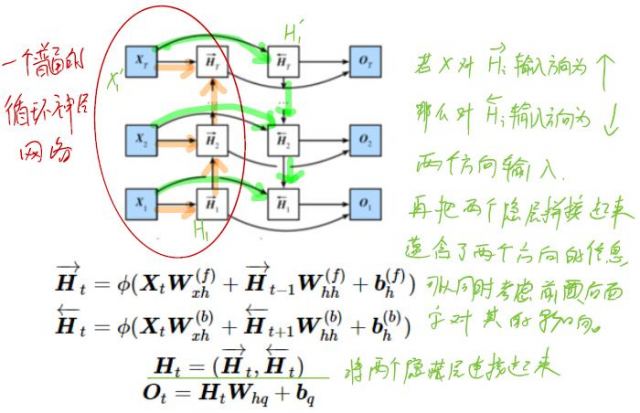
本文链接:http://task.lmcjl.com/news/5866.html