这是在ICLR 2018学术会议上发表的文章,其研究课题为交通网络的时空预测。
1.交通网络预测的具体问题描述如下:
在给定交通路网中有N个传感器实时监控该点的交通状况;根据其拓扑关系交通网络可表为一个含N个顶点的带权有向图G=(V,E,W)
W为N*N的带权邻接矩阵,权值为顶点间的“接近程度”。假设每个顶点所记录的交通状况可用一个P维的向量表示,那么整个路网在某一时刻的状况就可用一个N*P的矩阵表示。让X(t)代表时刻t时的交通状况矩阵;要训练出一个函数h(.),作用于过去T'个时间的矩阵,输出未来T个时刻的矩阵,做出交通预测。
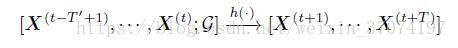
2.交通网络的预测难在复杂的时间和空间依赖性。
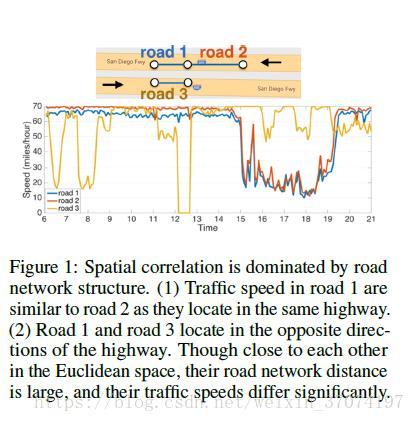
如图,同一道路的两个方向可能会有很大的差别,这说明在欧氏空间上挨的近的点不一定就相似。
空间结构是非欧氏且有向的。而长时间的时间依赖关系本身就是一个很难的问题。
3.交通路网预测的已有研究
近年来基于大数据的交通网预测是一个备受关注的课题。
自动回归模型、延时空间模型都不能很好地表达时间维度上的非线性依赖;直到循环神经网络的问世。
空间关系的处理上,CNN从简单的2D欧氏空间卷积到任意图的卷积(ChebNet),已经能够较好地表示图上的空间关系;但GCNN目前的成果都是基于无向图的;在有向的交通网络还不太适用。
本研究的主要内容就是进一步提出更合适的有向图上的卷积,并且和时间预测模型结合起来,提出扩散卷积的循环神经网络,在交通预测中获得比之前更好的效果。
4.实现:扩散卷积和循环神经网络的搭建

k表示扩散的步数。在此随机游走扩散引理的基础上,定义有向图上的扩散卷积:
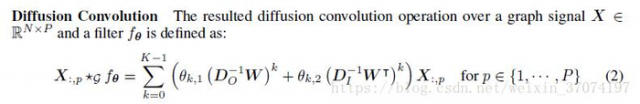
这是上面那个公式的扩展,因为考虑双向,使用两组独立的参数;另外由于其收敛特性,考虑到便于计算,一般取步数为一个有限的较小的K。

由此就可以对图上的每个顶点(交通特征)进行表示学习,将其映射到新的N*q矩阵H之中,参数量为2*K*P*Q.
建立基于时间的预测模型,本研究依然使用循环神经网络中的LSTM-GRU,因为它能非常好地处理长时依赖;不同的地方在于,GRU基本单元中各参数的计算改为扩散卷积的形式,取代了简单的可训练参数矩阵。

最后以DCGRU循环神经网络为基础建立seq to seq的编码解码网络。训练时使用scheduled sampling,逐渐地将decoder端的输入从真实数据换为预测数据。
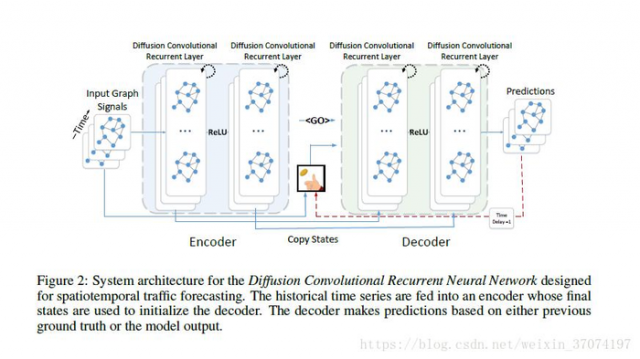
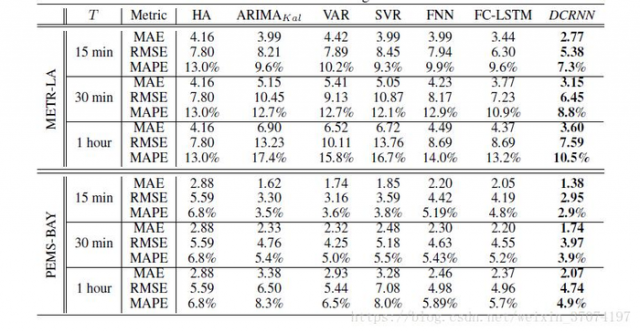
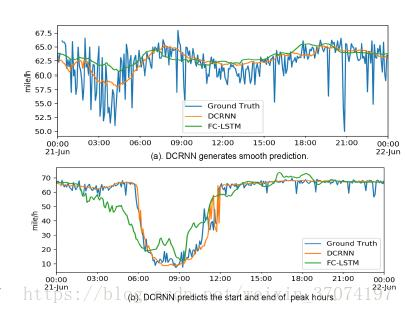
综上所述,该模型实现了时间空间上的兼顾,在两个大数据集上取得了由于之前研究的效果。
本文链接:http://task.lmcjl.com/news/720.html