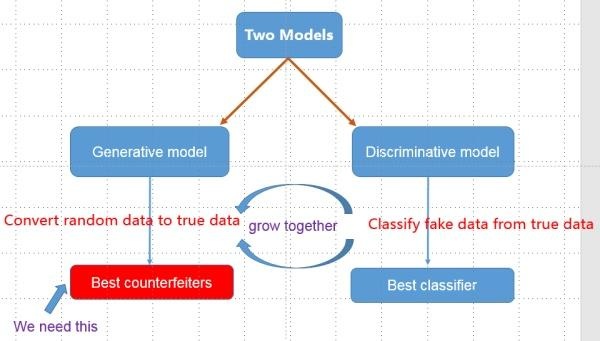
生成对抗网络分为:1.生成模型,2.鉴别模型。其中,生成模型从无到有不断地生成数据,而鉴别模型不断鉴别生成器生成的模型;二者不断对抗,生成模型拼命生成不让鉴别模型识别出来的数据,鉴别模型拼命鉴别生成模型生成的数据;二者不断成长,得到最好的生成模型和鉴别模型。
具体推倒如下:
首先是符号说明, 注意GAN,主要学习的是数据的分布,最终得到的是两个一样的数据分布。

定义数据分布,generator,discriminator等输出
定义鉴别模型:

当鉴别模型输出D(x)为1时,即可以轻松判别数据,此时上式取值最大。

当鉴别模型输出D(G(z))为0时,即鉴别模型轻松地鉴别出生成模型的数据,此时上式取值最大。
故而为了鉴别模型越来越好,定义以下目标函数:
很显然,最好的鉴别模型是使得V(G,D)最大的,即:

当鉴别模型取最好的时候,最好的生成模型即使得目标函数最小的,如下:
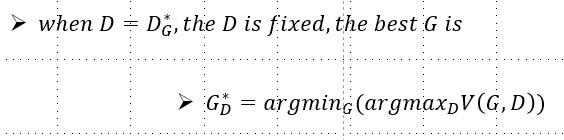
然后这个问题就转变成了最大最小问题:

这个问题真的有最优解吗?下面证明这个问题。
先证明有最优鉴别模型:

得到最优鉴别模型是
下面我们再来考虑一下GAN最终的目的是,得到生成模型可以生成非常逼真的数据,也就是说和真实数据分布一样的数据,此时鉴别模型的输出为:

其中,数据分布一样
当DG输出为0.5时,说明鉴别模型已经完全分不清真实数据和GAN生成的数据了,此时就是得到了最优生成模型了。
下面证明,生成模型存在:
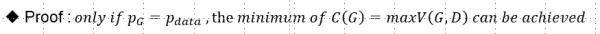
充分性:
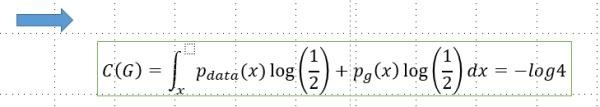
必要性:



上式最终可以转化为KL散度,如下:
KL散度永远大于等于0,可以知道目标函数最终最优值为-log4。
以上即是,GAN证明的推倒。
参考文献:
Goodfellow I, Pouget-Abadie J, Mirza M, et al. Generative adversarial nets[C]//Advances in neural information processing systems. 2014: 2672-2680.
An Annotated Proof
of Generative Adversarial Networks with Implementation Notes
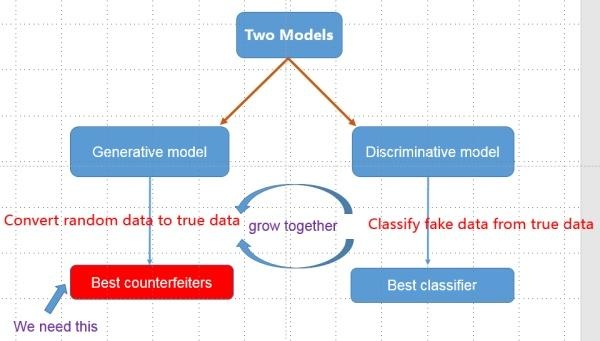
生成对抗网络分为:1.生成模型,2.鉴别模型。其中,生成模型从无到有不断地生成数据,而鉴别模型不断鉴别生成器生成的模型;二者不断对抗,生成模型拼命生成不让鉴别模型识别出来的数据,鉴别模型拼命鉴别生成模型生成的数据;二者不断成长,得到最好的生成模型和鉴别模型。
具体推倒如下:
首先是符号说明, 注意GAN,主要学习的是数据的分布,最终得到的是两个一样的数据分布。

定义数据分布,generator,discriminator等输出
定义鉴别模型:

当鉴别模型输出D(x)为1时,即可以轻松判别数据,此时上式取值最大。

当鉴别模型输出D(G(z))为0时,即鉴别模型轻松地鉴别出生成模型的数据,此时上式取值最大。
故而为了鉴别模型越来越好,定义以下目标函数:
很显然,最好的鉴别模型是使得V(G,D)最大的,即:

当鉴别模型取最好的时候,最好的生成模型即使得目标函数最小的,如下:
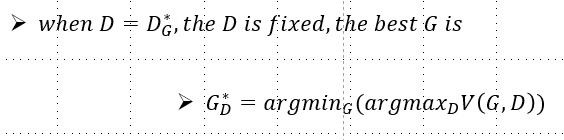
然后这个问题就转变成了最大最小问题:

这个问题真的有最优解吗?下面证明这个问题。
先证明有最优鉴别模型:

得到最优鉴别模型是
下面我们再来考虑一下GAN最终的目的是,得到生成模型可以生成非常逼真的数据,也就是说和真实数据分布一样的数据,此时鉴别模型的输出为:

其中,数据分布一样
当DG输出为0.5时,说明鉴别模型已经完全分不清真实数据和GAN生成的数据了,此时就是得到了最优生成模型了。
下面证明,生成模型存在:
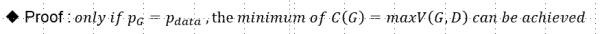
充分性:
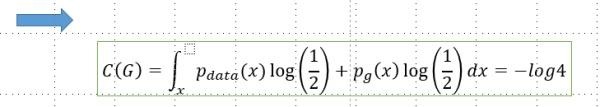
必要性:



上式最终可以转化为KL散度,如下:
KL散度永远大于等于0,可以知道目标函数最终最优值为-log4。
以上即是,GAN证明的推倒。
参考文献:
Goodfellow I, Pouget-Abadie J, Mirza M, et al. Generative adversarial nets[C]//Advances in neural information processing systems. 2014: 2672-2680.
An Annotated Proof
of Generative Adversarial Networks with Implementation Notes
本文链接:http://task.lmcjl.com/news/5363.html