循环神经网络——序列模型

关键词

循环神经网络——序列模型

文章目录

循环神经网络 Recurrent Neural Networks

前向传播
代价函数
反向传播

门控循环单元 GRU (gated recurrent units)
长短时记忆单元 LSTM (long short time memory)
双向RNN (bidirectional RNN)
深层RNN

循环神经网络 Recurrent Neural Networks

前向传播

many-to-many 结构
$\begin{matrix} {\hat{y}}^{< 1 >} & {\hat{y}}^{< 2 >} & {\hat{y}}^{< 3 >} & {\hat{y}}^{< T >} \\ ↑ & ↑ & ↑ & ↑ \\ a^{< 0 >} \to & \begin{matrix} ◯ \\ ◯ \\ ◯ \\ ◯ \end{matrix} & \overset{a^{< 1 >}}{\to} & \begin{matrix} ◯ \\ ◯ \\ ◯ \\ ◯ \end{matrix} & \overset{a^{< 2 >}}{\to} & \begin{matrix} ◯ \\ ◯ \\ ◯ \\ ◯ \end{matrix} & \to \dots \to & \begin{matrix} ◯ \\ ◯ \\ ◯ \\ ◯ \end{matrix} \\ ↑ & ↑ & ↑ & ↑ \\ x^{< 1 >} & x^{< 2 >} & x^{< 3 >} & x^{< T >} \end{matrix}$ a<0>→y^<1>↑◯◯◯◯↑x<1>a<1>y^<2>↑◯◯◯◯↑x<2>a<2>y^<3>↑◯◯◯◯↑x<3>→⋯→y^<T>↑◯◯◯◯↑x<T>

或者表示成：

$\begin{matrix} {\hat{y}}^{< 1 >} & {\hat{y}}^{< 2 >} & {\hat{y}}^{< T >} \\ ↑ & ↑ & ↑ \\ a^{< 0 >} \to & a^{< 1 >} & \to & a^{< 2 >} & \to \dots \to & a^{< T >} \\ ↑ & ↑ & ↑ \\ x^{< 1 >} & x^{< 2 >} & x^{< T >} \end{matrix}$ a<0>→y^<1>↑a<1>↑x<1>→y^<2>↑a<2>↑x<2>→⋯→y^<T>↑a<T>↑x<T>

数学表达式：
$\begin{matrix} a^{< 0 >} & = \vec{0} \\ a^{< 1 >} & = g_{1} (W_{a a} a^{< 0 >} + W_{a x} x^{< 1 >} + b_{a}) = g_{1} (W_{a} [a^{< 0 >}, x^{< 1 >}] + b_{a}) \\ y^{< 1 >} & = g_{2} (W_{y} a^{< 1 >} + b_{y}) \\ ⋮ \\ a^{< T >} & = g_{1} (W_{a a} a^{< T - 1 >} + W_{a x} x^{< T - 1 >} + b_{a}) = g_{1} (W_{a} [a^{< T - 1 >}, x^{< t >}] + b_{a}) \\ y^{< T >} & = g_{2} (W_{y} a^{< T >} + b_{y}) \end{matrix}$ a<0>a<1>y<1>⋮a<T>y<T>=0=g1(Waaa<0>+Waxx<1>+ba)=g1(Wa[a<0>,x<1>]+ba)=g2(Wya<1>+by)=g1(Waaa<T−1>+Waxx<T−1>+ba)=g1(Wa[a<T−1>,x<t>]+ba)=g2(Wya<T>+by) 其中，**函数 $g_{1}$ g1 通常取 tanh 或 relu， $g_{2}$ g2 取 sigmoid.

many-to-one 结构
例：输入一部影片，进行用户情感分析(喜欢/不喜欢)
$\begin{matrix} {\hat{y}}^{< T >} \\ ↑ \\ a^{< 0 >} \to & a^{< 1 >} & \to & a^{< 2 >} & \to \dots \to & a^{< T >} \\ ↑ & ↑ & ↑ \\ x^{< 1 >} & x^{< 2 >} & x^{< T >} \end{matrix}$ a<0>→a<1>↑x<1>→a<2>↑x<2>→⋯→y^<T>↑a<T>↑x<T>

one-to-one 结构
$\begin{matrix} \hat{y} \\ ↑ \\ a^{< 0 >} \to & a^{< 1 >} \\ ↑ \\ x \end{matrix}$ a<0>→y^↑a<1>↑x

one-to-many 结构：如音乐生成器
$\begin{matrix} {\hat{y}}^{< 1 >} & {\hat{y}}^{< 2 >} & {\hat{y}}^{< T >} \\ ↑ & ↑ & ↑ \\ a^{< 0 >} \to & a^{< 1 >} & \to & a^{< 2 >} & \to \dots \to & a^{< T >} \\ ↑ \\ x 或 ϕ \end{matrix}$ a<0>→y^<1>↑a<1>↑x或ϕ→y^<2>↑a<2>→⋯→y^<T>↑a<T>

其他many-to-many结构
$\begin{matrix} {\hat{y}}^{< 1 >} & {\hat{y}}^{< T_{y} >} \\ ↑ & ↑ \\ a^{< 0 >} \to & a^{< 1 >} & \to \dots \to & a^{< T_{x} >} & \to & a^{< T_{x} + 1 >} & \to \dots \to & a^{< T_{x} + T_{y} >} \\ ↑ & ↑ \\ x^{< 1 >} & x^{< T_{x} >} \end{matrix}$ a<0>→a<1>↑x<1>→⋯→a<Tx>↑x<Tx>→y^<1>↑a<Tx+1>→⋯→y^<Ty>↑a<Tx+Ty>

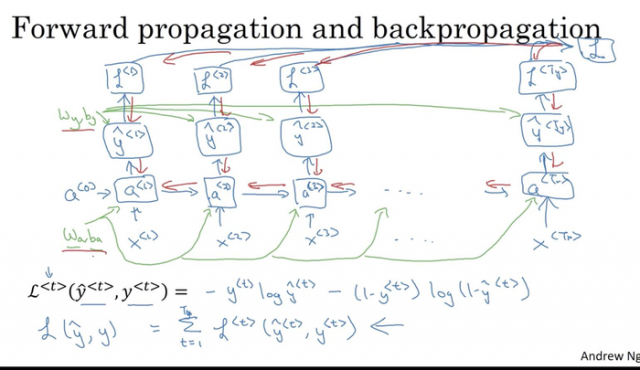
代价函数

$L (\hat{y}, y) = \sum_{t = 1}^{T} L^{< t >} ({\hat{y}}^{< t >}, y^{< t >})$ L(y^,y)=t=1∑TL<t>(y^<t>,y<t>) 其中， $L^{< t >} ({\hat{y}}^{< t >}, y^{< t >}) = - y^{< t >} \log {\hat{y}}^{< t >} - (1 - y^{< t >}) \log (1 - {\hat{y}}^{< t >})$ L<t>(y^<t>,y<t>)=−y<t>logy^<t>−(1−y<t>)log(1−y^<t>)

反向传播

仅以 many-to-many 为例：

门控循环单元 GRU (gated recurrent units)

解决梯度消失问题
c：memory cell
$\begin{matrix} {\tilde{c}}^{< t >} & = \tanh (W_{c} [Γ_{r} \times c^{< t - 1 >}, x^{< t >}] + b_{c}) \\ 相关门： Γ_{r} & = σ (W_{r} [c^{< t - 1 >}, x^{< t >}] + b_{r}) \\ 更新门： Γ_{u} & = σ (W_{u} [c^{< t - 1 >}, x^{< t >}] + b_{u}) \\ c^{< t >} & = Γ_{u} \times {\tilde{c}}^{< t >} + (1 - Γ_{u}) \times c^{< t - 1 >} \\ a^{< t >} & = c^{< t >} \end{matrix}$ c~<t>相关门：Γr更新门：Γuc<t>a<t>=tanh(Wc[Γr×c<t−1>,x<t>]+bc)=σ(Wr[c<t−1>,x<t>]+br)=σ(Wu[c<t−1>,x<t>]+bu)=Γu×c~<t>+(1−Γu)×c<t−1>=c<t> 当 $Γ_{u} \approx 1$ Γu≈1 时， $c^{< t >} \approx c^{< t - 1 >}$ c<t>≈c<t−1>.

长短时记忆单元 LSTM (long short time memory)

$\begin{matrix} {\tilde{c}}^{< t >} & = \tanh (W_{c} [a^{< t - 1 >}, x^{< t >}] + b_{c}) \\ 更新门： Γ_{u} & = σ (W_{u} [a^{< t - 1 >}, x^{< t >}] + b_{u}) \\ 遗忘门： Γ_{f} & = σ (W_{f} [a^{< t - 1 >}, x^{< t >}] + b_{f}) \\ 输出门： Γ_{o} & = σ (W_{o} [a^{< t - 1 >}, x^{< t >}] + b_{o}) \\ c^{< t >} & = Γ_{u} \times {\tilde{c}}^{< t >} + Γ_{f} \times c^{< t - 1 >} \\ a^{< t >} & = Γ_{o} \times c^{< t >} \end{matrix}$ c~<t>更新门：Γu遗忘门：Γf输出门：Γoc<t>a<t>=tanh(Wc[a<t−1>,x<t>]+bc)=σ(Wu[a<t−1>,x<t>]+bu)=σ(Wf[a<t−1>,x<t>]+bf)=σ(Wo[a<t−1>,x<t>]+bo)=Γu×c~<t>+Γf×c<t−1>=Γo×c<t>

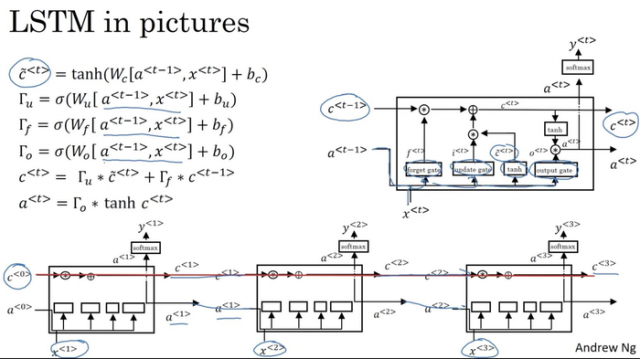
GRU or LSTM ?
GRU 只有两个门控，更简单，可以看成是LSTM的简化；
LSTM 有三个门控，更强大和灵活。

双向RNN (bidirectional RNN)

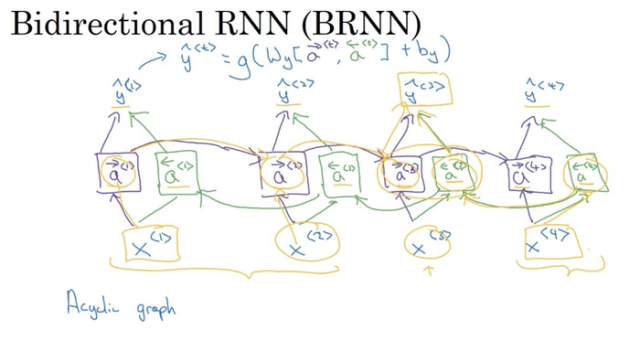
如对于输出 ${\hat{y}}^{< 3 >}$ y^<3>，即收到了来自过去 $x^{< 1 >}, x^{< 2 >}$ x<1>,x<2> 的信息，又收到了来自现在 $x^{< 3 >}$ x<3>，也收到了来自未来 $x^{< 4 >}$ x<4> 的信息。
在处理NLP问题中，带有LSTM的双向RNN是非常常用的。

深层RNN

$\begin{matrix} {\hat{y}}^{< 1 >} & {\hat{y}}^{< 2 >} & {\hat{y}}^{< T >} \\ ↑ & ↑ & ↑ \\ a^{[3] < 0 >} \to & a^{[3] < 1 >} & \to & a^{[3] < 2 >} & \to \dots \to & a^{[3] < T >} \\ ↑ & ↑ & ↑ \\ a^{[2] < 0 >} \to & a^{[2] < 1 >} & \to & a^{[2] < 2 >} & \to \dots \to & a^{[2] < T >} \\ ↑ & ↑ & ↑ \\ a^{[1] < 0 >} \to & a^{[1] < 1 >} & \to & a^{[1] < 2 >} & \to \dots \to & a^{[1] < T >} \\ ↑ & ↑ & ↑ \\ x^{< 1 >} & x^{< 2 >} & x^{< T >} \end{matrix}$ a[3]<0>→a[2]<0>→a[1]<0>→y^<1>↑a[3]<1>↑a[2]<1>↑a[1]<1>↑x<1>→→→y^<2>↑a[3]<2>↑a[2]<2>↑a[1]<2>↑x<2>→⋯→→⋯→→⋯→y^<T>↑a[3]<T>↑a[2]<T>↑a[1]<T>↑x<T>

如：其中 $a^{[2] < 2 >} = g (W_{a}^{[2]} [a^{[2] < 1 >]}, a^{[1] < 2 >}] + b^{[2]})$ a[2]<2>=g(Wa[2][a[2]<1>],a[1]<2>]+b[2])
当然，也可以把其中某些箭头去掉；每一个块不一定是标准的RNN，可以是LSTM或GRU；可以建立双向RNN.

本文链接：http://task.lmcjl.com/news/5573.html

展开阅读全文

上一篇：如何在pbootcms中制作静态化的TAG标签列表下一篇：基于keras中IMDB的文本分类 demo

热门文章排行

推荐文章

关键词

循环神经网络——序列模型

文章目录

循环神经网络 Recurrent Neural Networks

前向传播

代价函数

反向传播

门控循环单元 GRU (gated recurrent units)

长短时记忆单元 LSTM (long short time memory)

双向RNN (bidirectional RNN)

深层RNN