参考自：https://blog.csdn.net/sinat_42239797/article/details/90646935

1.卷积神经网络的结构

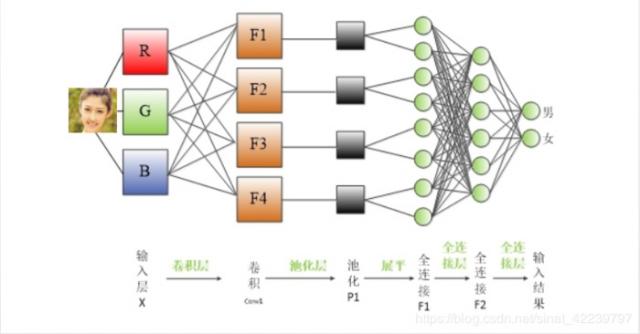
卷积神经网络（CNN）由输入层、卷积层、激活函数、池化层、全连接层组成，

即INPUT（输入层）-CONV（卷积层）-RELU（激活函数）-POOL（池化层）-FC（全连接层）

2.卷积神经网络的计算

计算公式为：

[N = (W-F+2P)/S+1
]

其中：

• N：输出大小
• W：输入大小
• F：卷积核大小
• P：填充值大小
• S：步长大小

比如：

nn.Conv2d(in_channels=3,out_channels=96,kernel_size=11,stride=4,padding=2)

卷积一层的几个参数：

• in_channels=3：表示输入的通道数。由于是RGB类型，所以通道数为3
• out_channels=96：表示输出的通道数，设定输出通道数的96（可以根据自己的需要来设置）
• kernel_size=12：表示卷积核的大小是12x12的，也就是上面的F=12
• stride=4：表示步长为4，也就是S=4
• padding=2：表示填充值的大小为2，也就是P=2

3.以AlexNet为例进行详解

AlexNet网络结构图如下图所示：

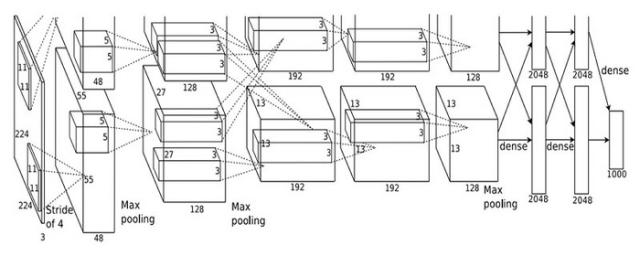
可以看出该网络有8层：5个卷积层，3个全连接层。

卷积神经网络的设置包括卷积层的设置以及正反向传播的设置
卷积层的设置代码如下：

self.conv1 = torch.nn.Sequential(   #input_size = 227*227*3
        torch.nn.Conv2d(in_channels=3,out_channels=96,kernel_size=11,stride=4,padding=0),
        torch.nn.ReLU(),
        torch.nn.MaxPool2d(kernel_size=3, stride=2) #output_size = 27*27*96
    )
self.conv2 = torch.nn.Sequential(   #input_size = 27*27*96
        torch.nn.Conv2d(96, 256, 5, 1, 2),
        torch.nn.ReLU(),
        torch.nn.MaxPool2d(3, 2)    #output_size = 13*13*256
    )
self.conv3 = torch.nn.Sequential(   #input_size = 13*13*256
        torch.nn.Conv2d(256, 384, 3, 1, 1),
        torch.nn.ReLU(),    #output_size = 13*13*384
    )
self.conv4 = torch.nn.Sequential(   #input_size = 13*13*384
        torch.nn.Conv2d(384, 384, 3, 1, 1),
        torch.nn.ReLU(),    #output_size = 13*13*384
    )
self.conv5 = torch.nn.Sequential(   #input_size = 13*13*384
        torch.nn.Conv2d(384, 256, 3, 1, 1),
        torch.nn.ReLU(),
        torch.nn.MaxPool2d(3, 2)    #output_size = 6*6*256
    )

self.dense = torch.nn.Sequential(
    torch.nn.Linear(9216, 4096),
    torch.nn.ReLU(),
    torch.nn.Dropout(0.5),
    torch.nn.Linear(4096, 4096),
    torch.nn.ReLU(),
    torch.nn.Dropout(0.5),
    torch.nn.Linear(4096, 50)
)

卷积一层

self.conv1 = torch.nn.Sequential(   #input_size = 227*227*3
            torch.nn.Conv2d(in_channels=3,out_channels=96,kernel_size=11,stride=4,padding=0),
            torch.nn.ReLU(),
            torch.nn.MaxPool2d(kernel_size=3, stride=2) #output_size = 27*27*96
        )

可以看到输入为227x227x3，也就是说size为227x227，通道数为3，为RGB图像。

torch.nn.Conv2d(in_channels=3,out_channels=96,kernel_size=11,stride=4,padding=0)

可以计算得到输出结果为：(N = (227-11+2times0)/4+1=55)，即卷积后的尺寸是55x55x96的。

torch.nn.ReLU()

使用激活函数ReLU，在神经元中的作用的：通过加权的输入进行非线性组合产生非线性决策边界。简单的来说就是增加非线性作用。

在深层卷积神经网络中使用激活函数同样也是增加非线性，主要是为了解决sigmoid函数带来的梯度消失问题。

 torch.nn.MaxPool2d(kernel_size=3, stride=2) #output_size = 27*27*96

MaxPool 最大池化层，池化层在卷积神经网络中的作用在于特征融合和降维。池化也是一种类似的卷积操作，只是池化层的所有参数都是超参数，是学习不到的。

这里的最大池化操作：将2x2尺寸内的所有像素值取最大值作为输出通道的像素值。

输出大小的计算和卷积层的计算过程一样：(N=(W-F+2P)/S+1=(55-3+2times0)/2+1=27)

则输出为27x27x96

卷积二层

self.conv2 = torch.nn.Sequential(   #input_size = 27*27*96
    torch.nn.Conv2d(96, 256, 5, 1, 2),
    torch.nn.ReLU(),
    torch.nn.MaxPool2d(3, 2)    #output_size = 13*13*256
)

可以看到卷积2层的输入为96x27x27的，也就是上一层的输出，从这里也就知道，上一层的输出为下一层的输入。

卷积2层的计算过程和卷积1层的计算过程是一样的，具体不详细描述
卷积2层最终输出为13x13x256，本层的神经元数目为27x27x256 =186642个
卷积3层最终输出为13x13x384，本层的神精元数目为13x13x384 =64896个
卷积4层最终输出为13x13x384，本层的神精元数目为13x13x384 = 64896个
卷积5层最终输出为6x6x256，本层的神精元数目为6x6x256=9216个

全连接层

全连接层的作用主要是负责逻辑推断，所有的参数都必须学习得到。

self.dense = torch.nn.Sequential(
        torch.nn.Linear(9216, 4096),
        torch.nn.ReLU(),
        torch.nn.Dropout(0.5),
        torch.nn.Linear(4096, 4096),
        torch.nn.ReLU(),
        torch.nn.Dropout(0.5),
        torch.nn.Linear(4096, 50)
    )

由结构图可以看到有3层全连接层

第一层全连接层（第六层）

作用：

1. 链接卷积层的输出
2. 去除空间信息（通道数），将三维矩阵转变为向量。

其操作可以看成是输入图像为(Wtimes Htimes C),卷积核的尺寸为(Wtimes Htimes C),这样卷积后的尺寸为(1times 1times 1),这样整个图像变成了一个数，一共有K个数（第一层全连接层后的神经元数）。

第六层输入数据的尺寸是6x6x256，采用6x6x256尺寸的滤波器对第六层的输入数据进行卷积运算；每个6x6x256尺寸的滤波器对第六层的输入数据进行卷积运算生成一个运算结果，通过一个神经元输出这个运算结果；共有4096个6x6x256尺寸的滤波器对输入数据进行卷积，通过4096个神经元的输出运算结果；然后通过ReLU激活函数以及dropout运算输出4096个本层的输出结果值。

第二层全连接层（第七层）

第6层输出的4096个数据与第7层的4096个神经元进行全连接，然后经由ReLU和Dropout进行处理后生成4096个数据。

第三层全连接层（第八层）

第7层输入的4096个数据与第8层的50个神经元进行全连接，经过训练后输出被训练的数值。

正向传播的顺序设置

def forward(self, x):   #正向传播过程
    conv1_out = self.conv1(x)
    conv2_out = self.conv2(conv1_out)
    conv3_out = self.conv3(conv2_out)
    conv4_out = self.conv4(conv3_out)
    conv5_out = self.conv5(conv4_out)
    '''
    x.view(x.size(0), -1)的用法：
	在CNN中，因为卷积或者池化之后需要连接全连接层，所以需要把多维度的tensor展平成一维，因此用它来实现(其实就是将多维数据展平为一维数据方便后面的全连接层处理)
    '''
    res = conv5_out.view(conv5_out.size(0), -1)
    out = self.dense(res)
    return out

常见的卷积层设置问题

1. 为什么是cove2d?

   cove1d：用于文本数据，只对宽度进行卷积，对高度不进行卷积
   cove2d：用于图像数据，对宽度和高度都进行卷积

2. 为什么卷积核大小5x5写一个5？

   Conv2d(输入通道数, 输出通道数, kernel_size（长和宽）)，当卷积核为方形时，只写一个就可以
   卷积核不是方形时，长和宽都要写：

   self.conv1 = nn.Conv2d(3, 6, (5,3))
   

3. 池化层的作用

   maxpooling有局部不变性而且可以提取显著特征的同时降低模型的参数，从而降低模型的过拟合。
   因为只是提取了显著特征，而舍弃了不显著的信息，使得模型的参数减少了，从而一定程度上可以缓解过拟合的产生。