本节讲解如何构建线性回归算法中的“线性模型”,所谓“线性”其实就是一条“直线”。因此,本节开篇首先普及一下初中的数学知识“一次函数”。
一次函数
一次函数就是最简单的“线性模型”,其直线方程表达式为
y = kx + b,其中 k 表示
斜率,b 表示
截距,x 为
自变量,y 表示
因变量。下面展示了 y = 2x + 3 的函数图像:
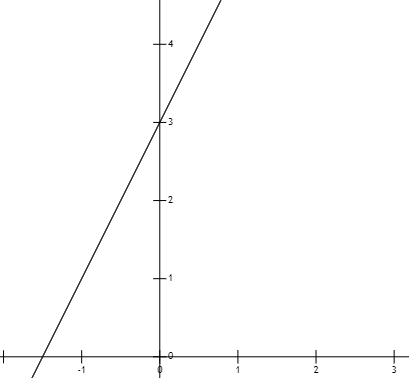
图1:函数图像y=2x+3
函数中斜率 k 与 截距 b 控制着“直线”的“旋转”与“平移”。如果斜率 k 逐渐减小,则“直线”会向着“顺时针”方向旋转,为 k= 0 的时候与 x 轴平行。截距 b 控制“直接”的上下平移,b 为正数则向上平移,b 为负数则表示向下平移。
在机器学习中斜率 k 通常用 w 表示,也就是权重系数,因此“线性方程”通过控制 w 与 b 来实现“直线”与数据点最大程度的“拟合”。如下图(黑色 x 号代表数据样本)所示:
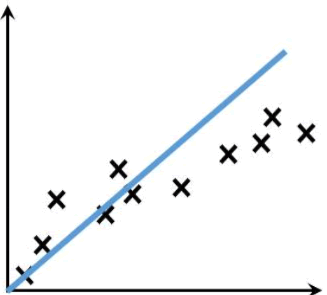
图2:线性拟合
线性方程不能完全等同于“直线方程”,因为前者可以描述多维空间内直接,而后者只能描述二维平面内的 x 与 y 的关系。
构建线性模型
在线性回归问题中数据样本会呈现“线性”分布的态势,因此我们使用“线性方程”来最大程度的“拟合数据”。线性方程预测的结果具有连续性,下面通过示例简单说明:小亮今年 8 岁,去年 7 岁,前年 6 岁,那么他明年几岁呢?估计你闭着眼都能想到答案,但是我们要从机器学习的角度去看待这个问题。
首先年龄、时间是一组连续性的数据,也就是因变量随着自变量规律性地连续增长,显然它是一个“回归问题”。下面把上述数据以二维数组的形式表示出来,构建一个数据集,如下所示:
[[2021,8],
[2020,7],
[2019,6]]
我们知道两个点就可以确定一条“直线”,因此将两组数据带入 y = kx + b,最终求得“线程方程”:
y = x - 2013
上述函数就是所谓的“假设函数”,通过它即可实现对结果的预测。这个函数的图像如下所示:
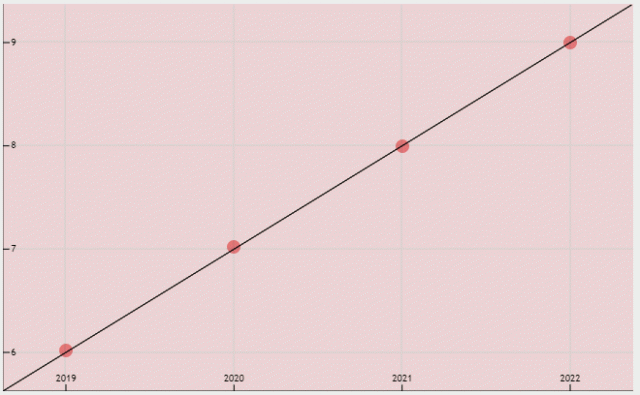
图3:假设函数图像
从上述函数图像可以看出,直线对数据样本恰好“拟合”。这是最标准的拟合直线,通过它就可以“预测”出小亮明年的年龄了。上述示例就构建了一个简单的的“线性模型”。读到这里你会惊叹“怎么如此简单”,其实线性模型就是这么简单。对于机器学习而言,最关键的就是“学习”,在大量的数据中,通过不断优化参数,找到一条最佳的拟合“直线”,最终预测出一个理想的结果。
提示:上述示例是一个理想化的“线性模型”,在实际应用中要复杂的多,不过“万变不离其宗”。
机器学习是一门数学、统计学、计算机科学的结合技术,因此它有着独特的知识体系,比如会将数据集分为“训练集”与“测试集”,而且还会通过“损失函数”来不断优化预测结果,关于这些知识会在后需内容详细介绍。
本文链接:http://task.lmcjl.com/news/15509.html


