目录
1. L1 Loss 平均绝对误差(Mean Absolute Error, MAE)
2. L2 Loss 均方误差损失(Mean Square Error, MSE)
交叉熵损失是基于“熵”这个概念,熵用来衡量信息的不确定性。对于概率分布为p(X)的随机变量X,熵可以表示为:
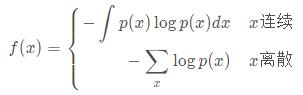
当X分布的不确定性越大,对应的熵越大(对应log(x)积分面积),反之,熵越小。
针对以上分析,可以把熵用于分类问题的损失,根据分类的类别数量不同,可以分为二元交叉熵损失和多分类交叉熵损失。
对于二分类问题(即0-1分类),即属于第1类的概率为p,属于第0类的概率为1−p。则二元交叉熵损失可表示为:
也可以统一写成如下形式:
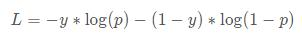
可以理解为:当实际类别为1时,我们希望预测为类别1的概率高一点,此时log(p)的值越小,产生的损失越小;反之,我们希望预测为类别0的概率高一点,此时log(1−p)的值越小,产生的损失也越小。
在实际应用中,二分类的类别概率通常采用sigmoid函数把结果映射到(0,1)之间。
对比二元交叉熵损失,可以推广到多分类交叉熵损失,定义如下:
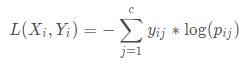

在多分类实际应用中,通常采用SoftMax函数来得到样本属于每个类别的概率。
Focal Loss首次在目标检测框架RetinaNet中提出,RetinaNet可以参考
它是对典型的交叉信息熵损失函数的改进,主要用于样本分类的不平衡问题。为了统一正负样本的损失函数表达式,首先做如下定义:

L1 loss即平均绝对误差(Mean Absolute Error, MAE),指模型预测值和真实值之间距离的平均值。

L2 loss即均方误差损失(Mean Square Error, MSE),指预测值和真实值之差的平方的平均值。

Smooth L1 loss是基于L1 loss修改得到,对于单个样本,记x为预测值和真实值的差值,则对应的Smooth L1 loss可表示为:
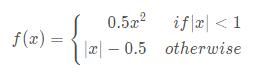
IoU类的损失函数都是基于预测框和标注框之间的IoU(交并比),记预测框为P,标注框为G,则对应的IoU可表示为:
即两个框的交集和并集的比值。IoU loss定义为:
IoU反映了两个框的重叠程度,在两个框不重叠时,IoU衡等于0,此时IoU loss恒等于1。而在目标检测的边界框回归中,这显然是不合适的。因此,GIoU loss在IoU loss的基础上考虑了两个框没有重叠区域时产生的损失。具体定义如下:
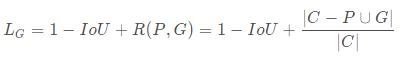
其中,C表示两个框的最小包围矩形框,R(P,G)是惩罚项。从公式可以看出,当两个框没有重叠区域时,IoU为0,但R依然会产生损失。极限情况下,当两个框距离无穷远时,R→1
IoU loss和GIoU loss都只考虑了两个框的重叠程度,但在重叠程度相同的情况下,我们其实更希望两个框能挨得足够近,即框的中心要尽量靠近。因此,DIoU在IoU loss的基础上考虑了两个框的中心点距离,具体定义如下:
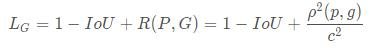
其中,ρ表示预测框和标注框中心端的距离,p和g是两个框的中心点。c表示两个框的最小包围矩形框的对角线长度。当两个框距离无限远时,中心点距离和外接矩形框对角线长度无限逼近,R→1
下图直观显示了不同情况下的IoU loss、GIoU loss和DIoU loss结果:
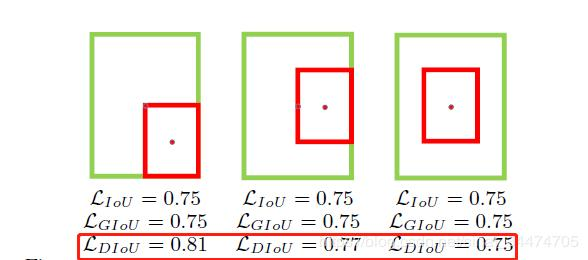
其中,绿色框表示标注框,红色框表示预测框,可以看出,最后一组的结果由于两个框中心点重合,检测效果要由于前面两组。IoU loss和GIoU loss的结果均为0.75,并不能区分三种情况,而DIoU loss则对三种情况做了很好的区分。
DIoU loss考虑了两个框中心点的距离,而CIoU loss在DIoU loss的基础上做了更详细的度量,具体包括:
具体定义如下:
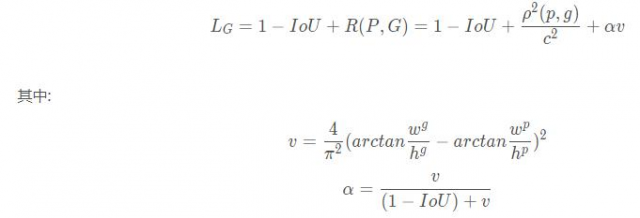

注:关于IoU系列损失更详细的分析可以参考论文:Distance-IoU Loss: Faster and Better Learning for Bounding Box Regression
本文链接:http://task.lmcjl.com/news/5428.html